Continuous Quality Improvement Cause And Effect Examples

Continuous Quality Improvement Cause And Effect Examples The continuous extension of f(x) f (x) at x = c x = c makes the function continuous at that point. can you elaborate some more? i wasn't able to find very much on "continuous extension" throughout the web. how can you turn a point of discontinuity into a point of continuity? how is the function being "extended" into continuity? thank you. And, because this is not right continuous, this is not a valid cdf function for any random variable. of course, the cdf of the always zero random variable 0 0 is the right continuous unit step function, which differs from the above function only at the point of discontinuity at x = 0 x = 0.

Continuous Quality Improvement Cause And Effect Examples Following is the formula to calculate continuous compounding a = p e^(rt) continuous compound interest formula where, p = principal amount (initial investment) r = annual interest rate (as a. The pasting lemma for finitely many closed sets now says that h h is continuous on x x. (a) would follow from the following lemma: if y y is an ordered topological space, l = {(y,y′) ∈y2: y ≤y′} l = {(y, y) ∈ y 2: y ≤ y} is closed in y2 y 2. assuming this lemma, (a) follows from standard facts on the product topology:. 3 this property is unrelated to the completeness of the domain or range, but instead only to the linear nature of the operator. yes, a linear operator (between normed spaces) is bounded if and only if it is continuous. Are there any examples of functions that are continuous, yet not differentiable? the other way around seems a bit simpler a differentiable function is obviously always going to be continuous.

Continous Quality Improvement Made Possible Pdf Patient Influenza 3 this property is unrelated to the completeness of the domain or range, but instead only to the linear nature of the operator. yes, a linear operator (between normed spaces) is bounded if and only if it is continuous. Are there any examples of functions that are continuous, yet not differentiable? the other way around seems a bit simpler a differentiable function is obviously always going to be continuous. 72 i found this comment in my lecture notes, and it struck me because up until now i simply assumed that continuous functions map closed sets to closed sets. what are some insightful examples of continuous functions that map closed sets to non closed sets?. For a continuous random variable x x, because the answer is always zero. note that there are also mixed random variables that are neither continuous nor discrete. that is, they take on uncountably many values, but do not have a continuous cumulative distribution function. these three types of random variables cover all possibilities though. Closure and continuous map ask question asked 6 years, 10 months ago modified 6 years, 10 months ago. Continuous spectrum: the continuous spectrum exists wherever ω(λ) ω (λ) is positive, and you can see the reason for the original use of the term continuous spectrum. you have an integral sum of eigenfunctions over a continuous range of eigenvalues. later, the definition evolved in order to study this is a more abstract setting.

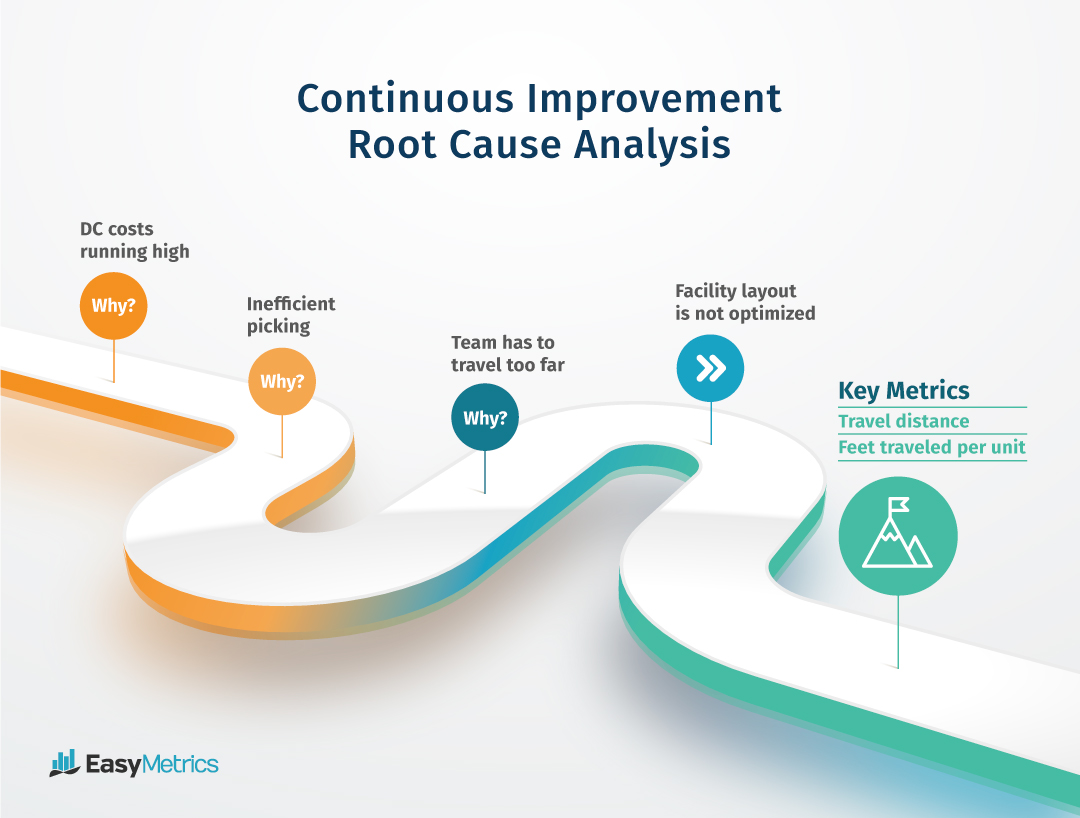
Kaizen Continuous Improvement Examples 72 i found this comment in my lecture notes, and it struck me because up until now i simply assumed that continuous functions map closed sets to closed sets. what are some insightful examples of continuous functions that map closed sets to non closed sets?. For a continuous random variable x x, because the answer is always zero. note that there are also mixed random variables that are neither continuous nor discrete. that is, they take on uncountably many values, but do not have a continuous cumulative distribution function. these three types of random variables cover all possibilities though. Closure and continuous map ask question asked 6 years, 10 months ago modified 6 years, 10 months ago. Continuous spectrum: the continuous spectrum exists wherever ω(λ) ω (λ) is positive, and you can see the reason for the original use of the term continuous spectrum. you have an integral sum of eigenfunctions over a continuous range of eigenvalues. later, the definition evolved in order to study this is a more abstract setting.

Enter a world where style is an expression of individuality. From fashion trends to style tips, we're here to ignite your imagination, empower your self-expression, and guide you on a sartorial journey that exudes confidence and authenticity in our Continuous Quality Improvement Cause And Effect Examples section.

How to create cause-and-effect diagrams

How to create cause-and-effect diagrams

How to create cause-and-effect diagrams Whiteboard: Cause and Effect Diagrams Fishbone (Cause & Effect or Ishikawa Diagram) The 7 Quality Control (QC) Tools Explained with an Example! Continuous Improvement 18 - Creating a Cause and Effect Diagram - Value Generation Partners Identifying Root Causes Cause and Effect Diagram Training Video (aka Fishbone Diagram & Ishikawa Diagram) PDCA TOOLS AND TECHNIQUES Part 1 ISO 14001:2015 Awareness Training (Full) #iso14001 #environmentalmanagement #esg #sustainability Tools #2: Example of a Cause and Effect Diagram STOP Making These Mistakes with Cause and Effect Analysis PMP - Cause-and-Effect Diagrams & Pareto Diagrams Continuous Quality Improvement for Fall Prevention How to use Fishbone Diagram Step by Step: Simple Cause-and-Effect Tool I Explainer Fishbone / Ishikawa / Cause and effect diagram The 5 Why's Explained | Root Cause Analysis | Quality Management Certification | Invensis Learning Ishikawa diagram Fishbone diagram Cause Effect Why Why Diagram Quality tools for PMP exam Fishbone Diagram Tool for Root Cause Analysis | Ishikawa Diagram | Cause-and-effect Diagrams How Are Cause And Effect Diagrams Helpful In Production? - The Friendly Statistician Fishbone Diagram । Cause and effect diagram । Ishikawa Diagram (One of 7 basic quality Control tool)

Conclusion

Considering all the aspects, there is no doubt that publication presents beneficial understanding touching on Continuous Quality Improvement Cause And Effect Examples. From beginning to end, the creator manifests an impressive level of expertise on the topic. Significantly, the review of important characteristics stands out as particularly informative. The article expertly analyzes how these features complement one another to establish a thorough framework of Continuous Quality Improvement Cause And Effect Examples.

On top of that, the piece does a great job in simplifying complex concepts in an easy-to-understand manner. This clarity makes the analysis useful across different knowledge levels. The author further improves the investigation by including applicable models and actual implementations that help contextualize the intellectual principles.

A further characteristic that makes this piece exceptional is the comprehensive analysis of multiple angles related to Continuous Quality Improvement Cause And Effect Examples. By investigating these various perspectives, the content gives a objective understanding of the topic. The completeness with which the content producer approaches the matter is genuinely impressive and offers a template for analogous content in this subject.

To summarize, this piece not only enlightens the reader about Continuous Quality Improvement Cause And Effect Examples, but also stimulates additional research into this interesting theme. If you are just starting out or an experienced practitioner, you will uncover valuable insights in this comprehensive write-up. Thank you for this detailed article. If you need further information, feel free to drop a message through the comments section below. I am eager to your feedback. For more information, you can see various relevant pieces of content that are interesting and complementary to this discussion. Happy reading!