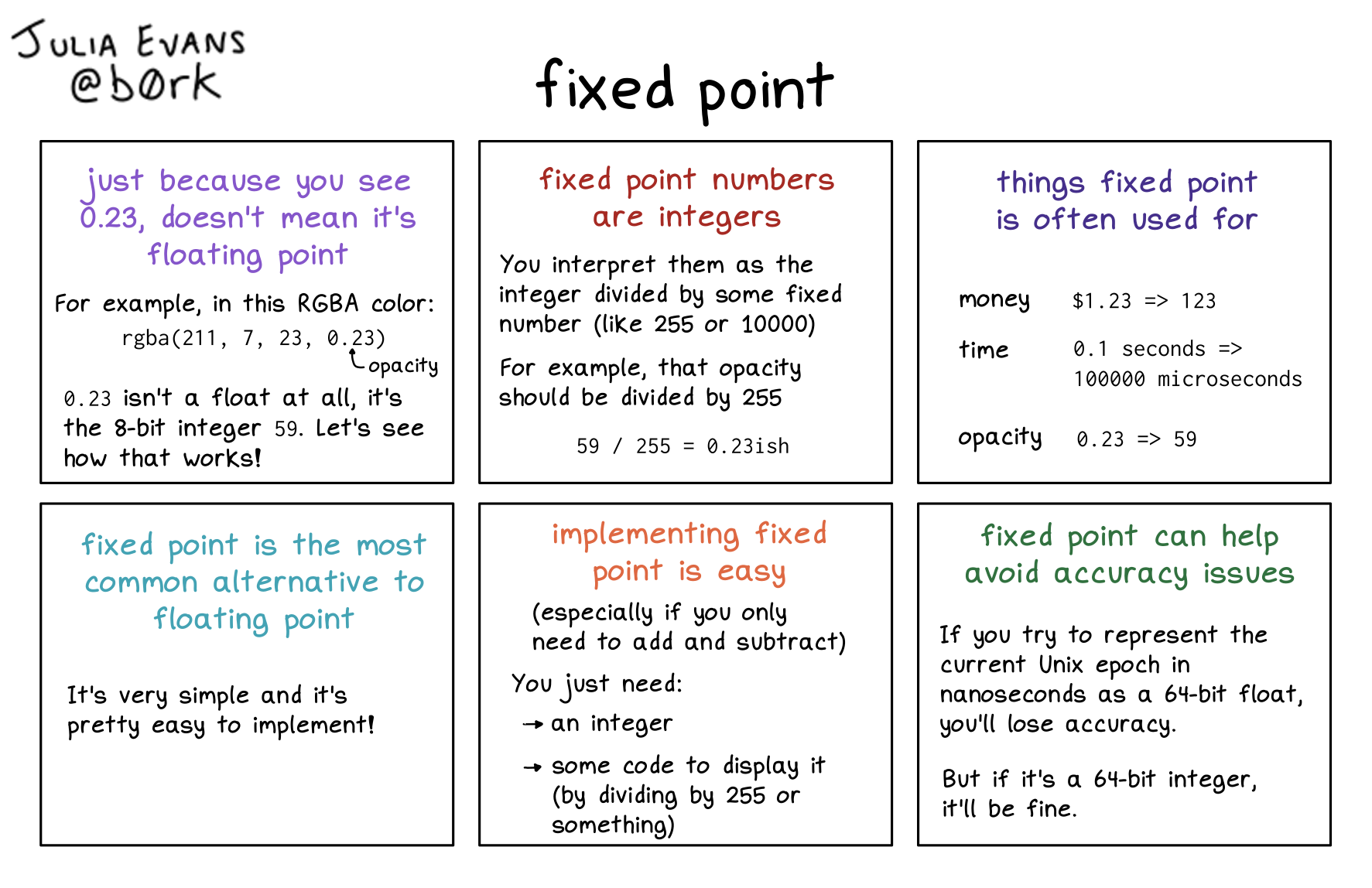
Fixed Point A fixed point is a value that does not change under a given transformation, such as a function or a group action. learn about fixed point theorems, iteration, properties, applications, and logics in mathematics and computer science. A fixed point is a point that does not change under a map, function or system of equations. learn how to find fixed points using wolfram language commands and see examples of fixed points in trigonometric, hyperbolic and complex functions.

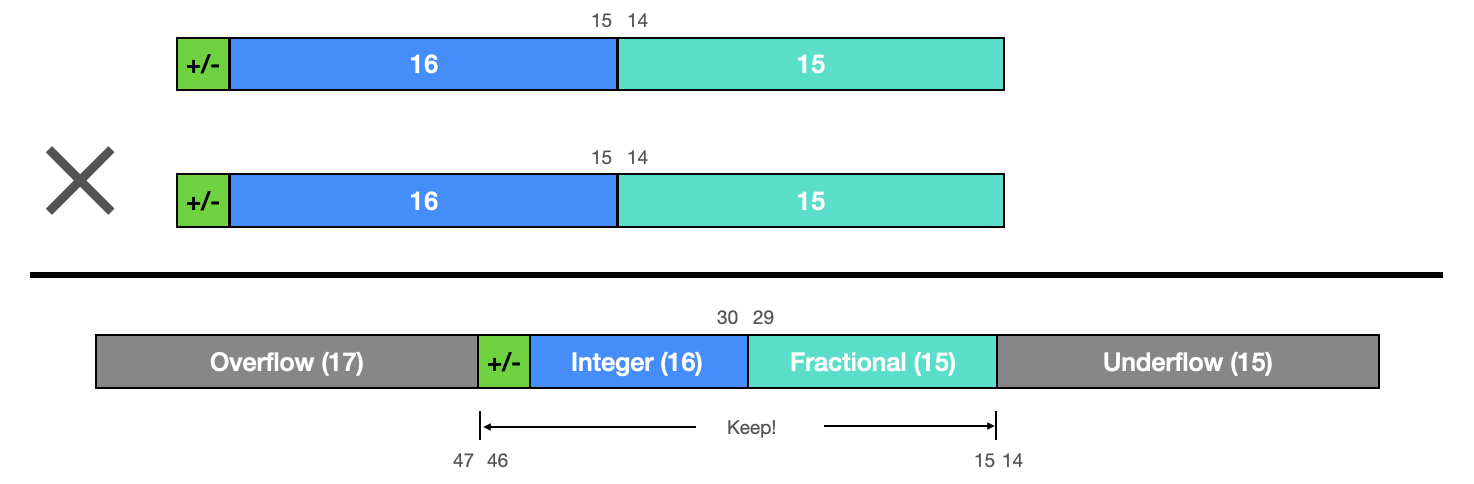
Fixedpoint A fixed point is said to be stable if a small perturbation of the solution from the fixed point decays in time; it is said to be unstable if a small perturbation grows in time. A fixed point of a mapping $ f $ on a set $ x $ is a point $ x \\in x $ for which $ f ( x) = x $. learn about various fixed point principles and their applications to equations, operators, vector fields and more. Fixed point is a representation of real data type for a number that has a fixed number of digits after the radix point. floating point is a formulaic representation of real numbers as an approximation so as to support a tradeoff between range and precision. A fixed point of a function is an input the function maps to itself. when we study the fixed points of a function, we can learn many interesting things about the function itself. this first of four parts defines fixed points, and looks at a few examples.

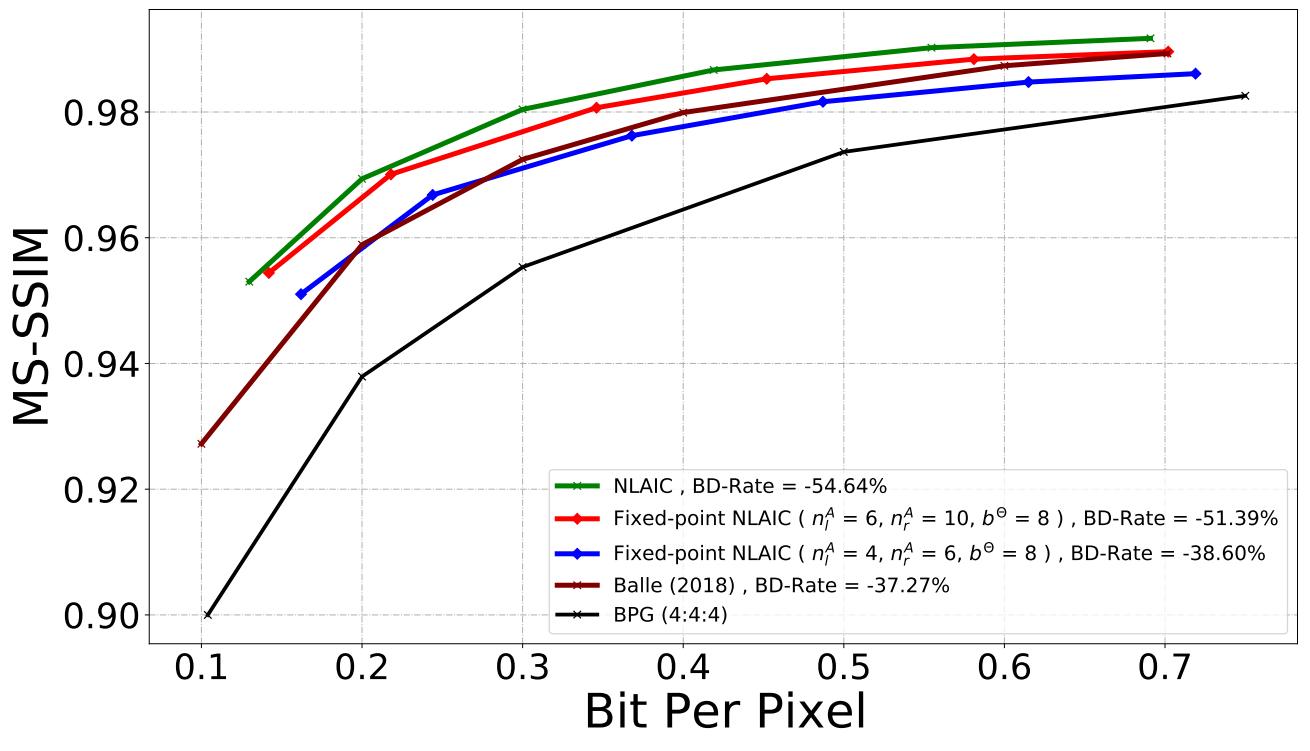
Fixed Point Convolution Framework Fixed Point Fixed point is a representation of real data type for a number that has a fixed number of digits after the radix point. floating point is a formulaic representation of real numbers as an approximation so as to support a tradeoff between range and precision. A fixed point of a function is an input the function maps to itself. when we study the fixed points of a function, we can learn many interesting things about the function itself. this first of four parts defines fixed points, and looks at a few examples. The contraction mapping theorem says that if a function h is a contraction mapping on a closed interval, then h has a unique fixed point. you can generalize this from working on closed interval to working in any complete metric space. Learn the difference between equilibrium point and fixed point in mathematics and other fields. equilibrium point is a solution of a differential equation where the rate of change is zero, while fixed point is a point in a function where the output is equal to the input. Fixed point arithmetic is a method of representing fractional numbers by storing a fixed number of digits of their fractional part. learn how fixed point numbers are represented, scaled, and used in computing, and compare them with floating point numbers. Fixed point theorem statement: let f: [a, b] → [a, b] be a continuous function. then f has a fixed point, that is, ∃ a point c ∈ (a, b) such that f (c) = c. proof: if either f (a)=a or f (b)=b or both are true, then there is nothing to prove. so we assume that f (a) > a and f (b) < b. now, we define the function.

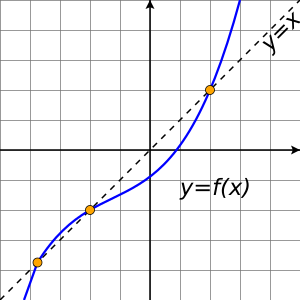
Fixed Point Facts For Kids The contraction mapping theorem says that if a function h is a contraction mapping on a closed interval, then h has a unique fixed point. you can generalize this from working on closed interval to working in any complete metric space. Learn the difference between equilibrium point and fixed point in mathematics and other fields. equilibrium point is a solution of a differential equation where the rate of change is zero, while fixed point is a point in a function where the output is equal to the input. Fixed point arithmetic is a method of representing fractional numbers by storing a fixed number of digits of their fractional part. learn how fixed point numbers are represented, scaled, and used in computing, and compare them with floating point numbers. Fixed point theorem statement: let f: [a, b] → [a, b] be a continuous function. then f has a fixed point, that is, ∃ a point c ∈ (a, b) such that f (c) = c. proof: if either f (a)=a or f (b)=b or both are true, then there is nothing to prove. so we assume that f (a) > a and f (b) < b. now, we define the function.