5 Hash Table Datastructure Pdf Time Complexity Function Mathematics Has detailed articles on hash tables and cryptographic hash functions. what are you looking for that isn't in those?. The main difference between hash functions and pseudorandom number generators is that a hash function gives a unique value for each input. this is important for applications such as hash tables and message verification: in hash tables, a hash function is used to choose the location at which an input is put.

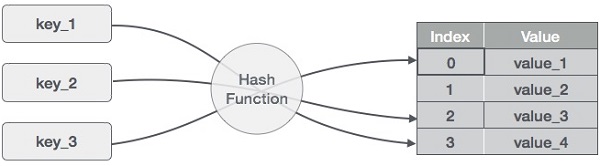
Data Structure And Algorithms Hash Table 由于他的调皮，导致客户挑妹纸的时间大幅延长，从10秒到了800秒。 在代码中，一般都有一些比较复杂的算法去运算而得出这个hash值，一旦破解了这个算法，就又可以调皮啦。 在java中，hash算法在hashmap中有体现，有兴趣的可以去看看源码。. I am reading the "introduction to algorithms" by thomas cormen et al. particularly the theorem which says that given an open address hash table with load factor $\\alpha = n m < 1$, the expected. The one omitted hash value (all 1's, or sometimes remapped as all 0's) can be used as a special sentinel value for "empty hash bucket". it turns out this is equivalent to 1's complement arithmetic, which is often used in hash algorithms like fletcher for this reason. The biggest advantage of hashing vs. binary search is that it is much cheaper to add or remove an item from a hash table, compared to adding or removing an item to a sorted array while keeping it sorted. (binary search trees work a bit better in that respect).

Understanding Hash Tables Data Structures Collision Resolution The one omitted hash value (all 1's, or sometimes remapped as all 0's) can be used as a special sentinel value for "empty hash bucket". it turns out this is equivalent to 1's complement arithmetic, which is often used in hash algorithms like fletcher for this reason. The biggest advantage of hashing vs. binary search is that it is much cheaper to add or remove an item from a hash table, compared to adding or removing an item to a sorted array while keeping it sorted. (binary search trees work a bit better in that respect). For example, suppose we wish to allocate a hash table, with collisions resolved by chaining, to hold roughly n = 2000 n = 2000 character strings, where a character has 8 bits. we don't mind examining an average of 3 elements in an unsuccesful search, so we allocate a table of size m = 701 m = 701. Let's take a hash table where the collision problem is solved using a linked list. as we know, in the worst case, due to collisions, searching for an element in the hash table takes o (n). but why does deleting and inserting an element also take o (n)? we use a linked list where these operations are performed in o (1). 6 hash tables resolve collisions through two mechanisms, separate chaining or open hashing and open addressing or closed hashing. though the first method uses lists (or other fancier data structure) in hash table to maintain more than one entry having same hash values, the other uses complex ways of skipping n elements on collsion. A perfect hash would completely avoid any collision between passwords up to the length of the hash. for typical hash lengths, that means that collisions on passwords longer than the original are so rare that they simply preclude any brute force search.

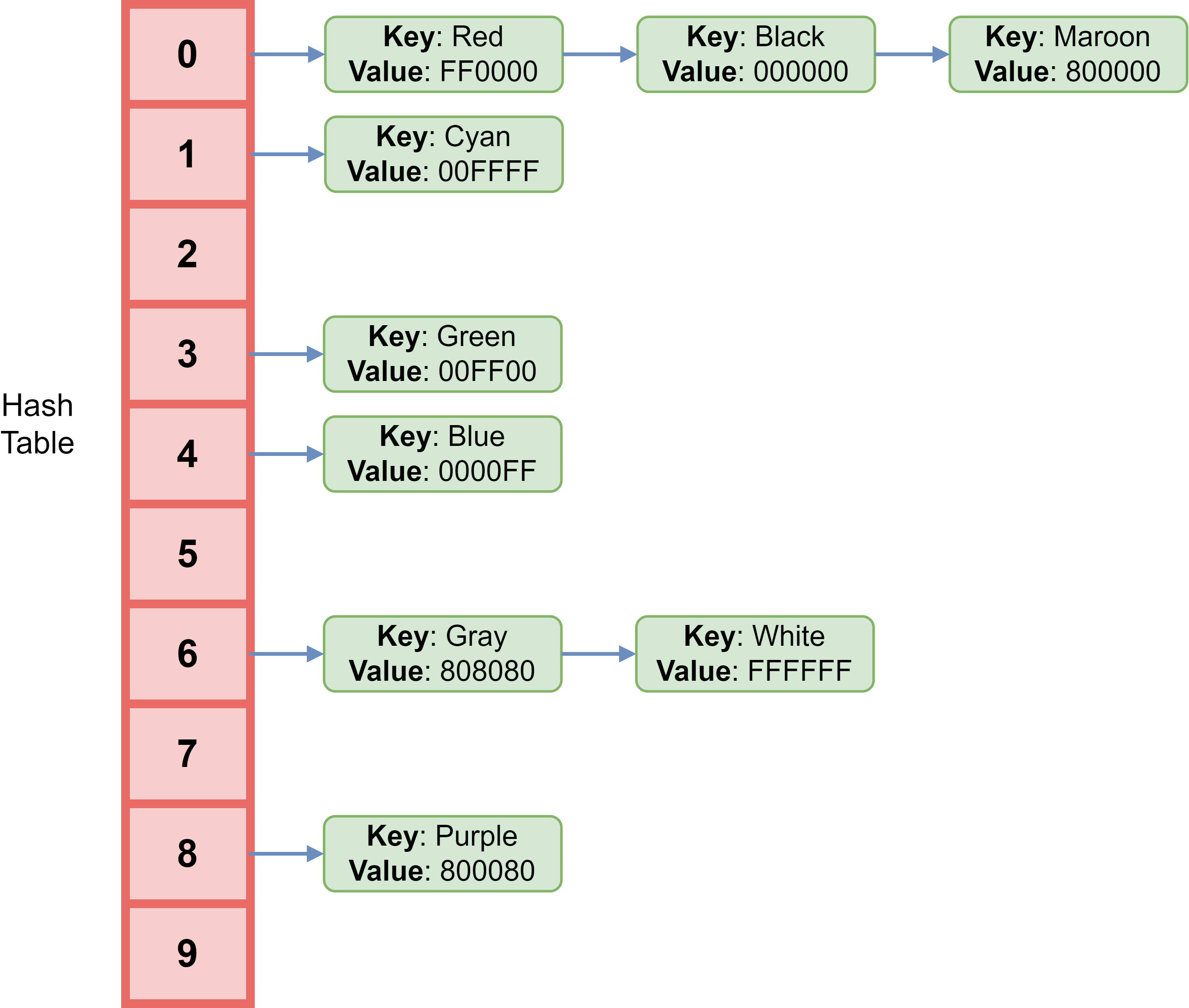
Data Structure Hash Table Bigboxcode For example, suppose we wish to allocate a hash table, with collisions resolved by chaining, to hold roughly n = 2000 n = 2000 character strings, where a character has 8 bits. we don't mind examining an average of 3 elements in an unsuccesful search, so we allocate a table of size m = 701 m = 701. Let's take a hash table where the collision problem is solved using a linked list. as we know, in the worst case, due to collisions, searching for an element in the hash table takes o (n). but why does deleting and inserting an element also take o (n)? we use a linked list where these operations are performed in o (1). 6 hash tables resolve collisions through two mechanisms, separate chaining or open hashing and open addressing or closed hashing. though the first method uses lists (or other fancier data structure) in hash table to maintain more than one entry having same hash values, the other uses complex ways of skipping n elements on collsion. A perfect hash would completely avoid any collision between passwords up to the length of the hash. for typical hash lengths, that means that collisions on passwords longer than the original are so rare that they simply preclude any brute force search.