
Detecting And Fixing Precision Specific Operations For Measuring Use fixed point designer to quickly identify numeric and indexing flaws in your algorithms, so you can find errors early in the process. this video walks through both fixed point and. Use fixed point designer™ to quickly identify numeric and indexing flaws in your algorithms, so you can find errors early in the process. this video walks through both fixed point and floating point examples.

How To Test For Numeric Errors In Floating And Fixed Point Algorithms Fixed point designer provides apps and tools for analyzing double precision algorithms and converting them to reduced precision floating point or fixed point. optimization tools enable you to select data types that meet your numerical accuracy requirements and target hardware constraints. For ieee, the single representation is 1 bit sign, 8 bit exponent and 23 bit mantissa. this means that at each exponent value, you can test all 2^23 1 (roughly 9mil cases) possible combination of binary representation (give or take). Given an function f that performs a numerical computation on 32 bit ieee 754 floating point numbers, what would be the (best) way to test if f is numerically stable? is there a black box test that does not need to know more about the function other than its argument types?. Roundoff errors and floating point arithmetic ä the basic problem: the set a of all possible representable numbers on a given machine is finite but we would like to use this set to perform standard arithmetic operations ( ,*, , ) on an infinite set.

Algorithms Go From Floating To Fixed Point Ee Times Given an function f that performs a numerical computation on 32 bit ieee 754 floating point numbers, what would be the (best) way to test if f is numerically stable? is there a black box test that does not need to know more about the function other than its argument types?. Roundoff errors and floating point arithmetic ä the basic problem: the set a of all possible representable numbers on a given machine is finite but we would like to use this set to perform standard arithmetic operations ( ,*, , ) on an infinite set. Use fixed point designer to quickly identify numeric and indexing flaws in your algorithms, so you can find errors early in the process. this video walks through both fixed point and floating point examples. This example shows how to start with a floating point design in matlab®, iteratively converge on an efficient fixed point design in matlab, and verify the numerical accuracy of the generated fixed point design. This guide shows you how to identify, prevent, and correct floating point errors in matlab to ensure accurate, reliable numerical results. scientists and engineers rely on matlab for critical calculations. even small computational errors can dramatically affect outcomes. If you're going to use a loop to multiply your number repeatedly, and then check whether the 1s digit is even or odd, you will likely run into inaccuracies. one slightly surprising way to find trouble is to check simple equality. consider the following java code: double x = 10.0; double y = 3.0; system.out.println( (1*x (y*1)) == (10*x (y*10)) );.
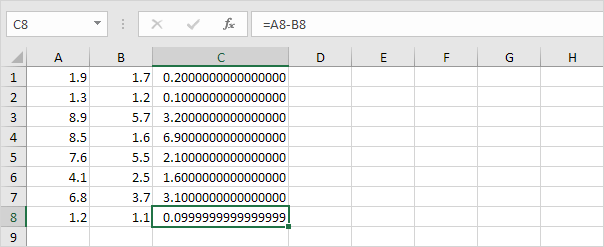
Floating Point Errors In Excel Easy Excel Tutorial Use fixed point designer to quickly identify numeric and indexing flaws in your algorithms, so you can find errors early in the process. this video walks through both fixed point and floating point examples. This example shows how to start with a floating point design in matlab®, iteratively converge on an efficient fixed point design in matlab, and verify the numerical accuracy of the generated fixed point design. This guide shows you how to identify, prevent, and correct floating point errors in matlab to ensure accurate, reliable numerical results. scientists and engineers rely on matlab for critical calculations. even small computational errors can dramatically affect outcomes. If you're going to use a loop to multiply your number repeatedly, and then check whether the 1s digit is even or odd, you will likely run into inaccuracies. one slightly surprising way to find trouble is to check simple equality. consider the following java code: double x = 10.0; double y = 3.0; system.out.println( (1*x (y*1)) == (10*x (y*10)) );.
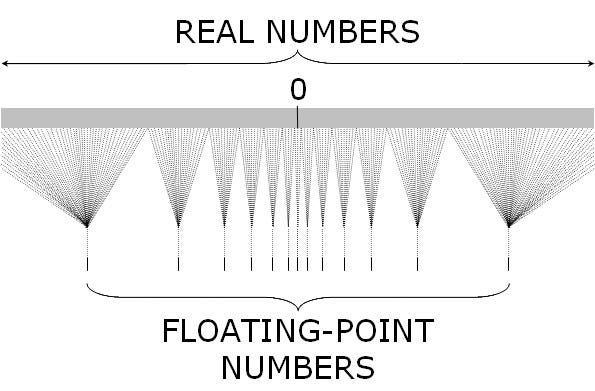
Mitigating Floating Point Errors In Computational Geometry Algorithms This guide shows you how to identify, prevent, and correct floating point errors in matlab to ensure accurate, reliable numerical results. scientists and engineers rely on matlab for critical calculations. even small computational errors can dramatically affect outcomes. If you're going to use a loop to multiply your number repeatedly, and then check whether the 1s digit is even or odd, you will likely run into inaccuracies. one slightly surprising way to find trouble is to check simple equality. consider the following java code: double x = 10.0; double y = 3.0; system.out.println( (1*x (y*1)) == (10*x (y*10)) );.