Logarithm Rules Example

Rules Of Logarithm Pdf The laws of logarithms are algebraic rules that allow for the simplification and rearrangement of logarithmic expressions. the 3 main logarithm laws are: the product law: log (mn) = log (m) log (n). the quotient law: log (m n) = log (m) – log (n). the power law: log (m k) = k·log (m). the three fundamental laws of logarithms are shown below. Learn the eight (8) log rules or laws to help you evaluate, expand, condense, and solve logarithmic equations. try out the log rules practice problems for an even better understanding.

Logarithm Rules Example Logarithm rules are used to simplify and work with logarithmic expressions. they help relate logarithms to exponents and make complex calculations easier. a logarithm is the inverse of an exponent. it answers the question: "to what power must a base be raised to get a certain number?". Understand the concept of logarithmic functions and how to apply logarithm rules such as product, quotient and power rule. Logarithm rules are the properties or the identities of the logarithm that are used to simplify complex logarithmic expressions and solve logarithmic equations involving variables. Logarithm, the exponent or power to which a base must be raised to yield a given number. expressed mathematically, x is the logarithm of n to the base b if bx = n, in which case one writes x = log b n. for example, 2 3 = 8; therefore, 3 is the logarithm of 8 to base 2, or 3 = log 2 8. in the same fashion, since 10 2 = 100, then 2 = log 10 100.

Logarithm Rules Properties With Examples Logarithm rules are the properties or the identities of the logarithm that are used to simplify complex logarithmic expressions and solve logarithmic equations involving variables. Logarithm, the exponent or power to which a base must be raised to yield a given number. expressed mathematically, x is the logarithm of n to the base b if bx = n, in which case one writes x = log b n. for example, 2 3 = 8; therefore, 3 is the logarithm of 8 to base 2, or 3 = log 2 8. in the same fashion, since 10 2 = 100, then 2 = log 10 100. Scroll down the page for more explanations and examples on how to use the rules to simplify and expand logarithmic expressions. the rules of logarithms are: the logarithm of a product is the sum of the logarithms of the factors. log a xy = log a x log a y. The base b logarithm of a number is the exponent that we need to raise the base in order to get the number. the logarithm of the multiplication of x and y is the sum of logarithm of x and logarithm of y. the logarithm of the division of x and y is the difference of logarithm of x and logarithm of y. There are mainly 4 important log rules which are stated as follows: the following log rules are derived from the formula of logarithmic form to exponential form and vice versa (b x = m ⇔ log b m = x). along with these rules, we have several other rules of logarithms. all logarithm rules are mentioned below:. This page covers all 8 log rules (including the change of base formula and log exponent rules). each log rule is covered in depth with simple explanations and examples.

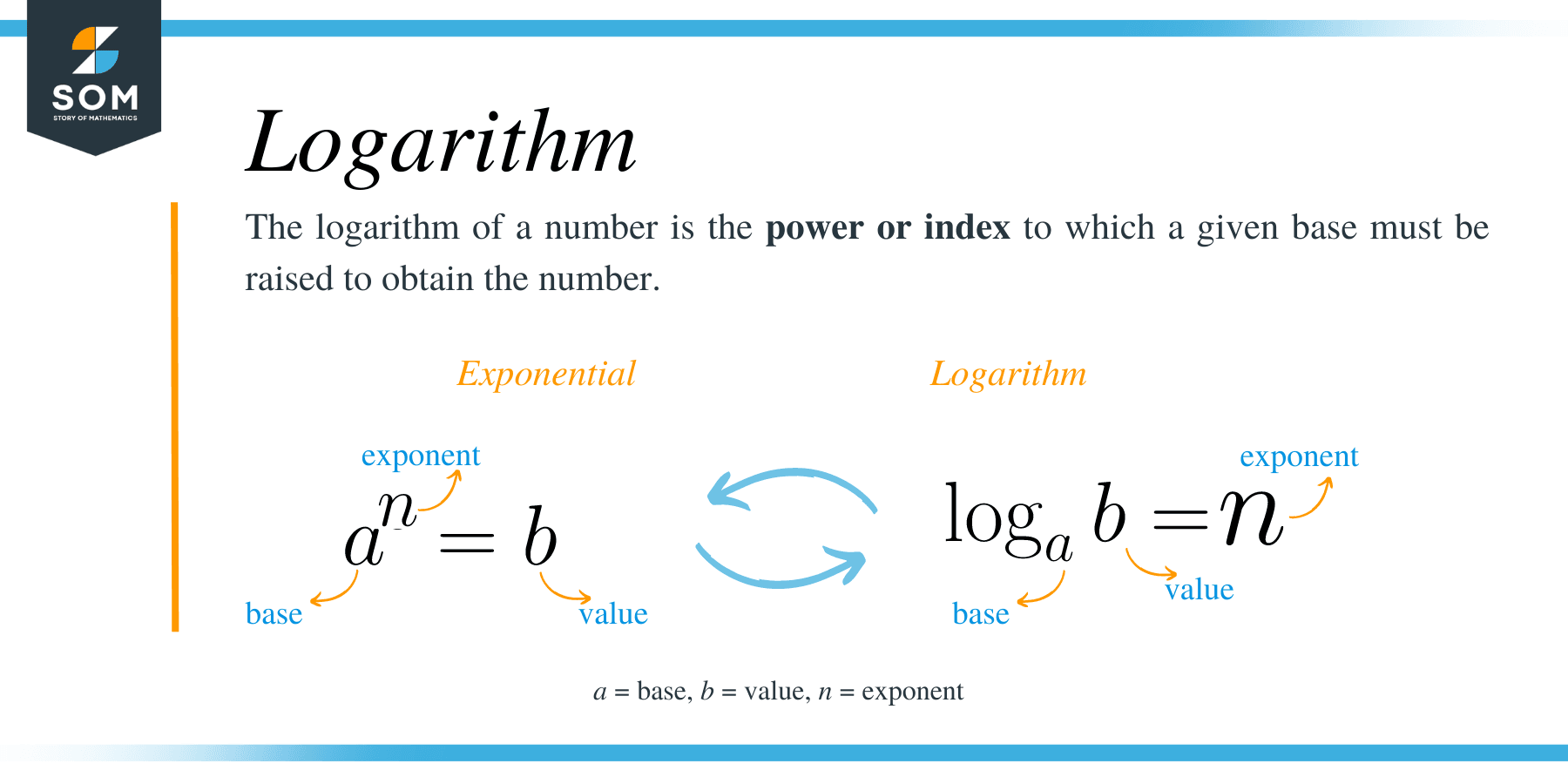
Logarithm Rules Explanation Examples Scroll down the page for more explanations and examples on how to use the rules to simplify and expand logarithmic expressions. the rules of logarithms are: the logarithm of a product is the sum of the logarithms of the factors. log a xy = log a x log a y. The base b logarithm of a number is the exponent that we need to raise the base in order to get the number. the logarithm of the multiplication of x and y is the sum of logarithm of x and logarithm of y. the logarithm of the division of x and y is the difference of logarithm of x and logarithm of y. There are mainly 4 important log rules which are stated as follows: the following log rules are derived from the formula of logarithmic form to exponential form and vice versa (b x = m ⇔ log b m = x). along with these rules, we have several other rules of logarithms. all logarithm rules are mentioned below:. This page covers all 8 log rules (including the change of base formula and log exponent rules). each log rule is covered in depth with simple explanations and examples.

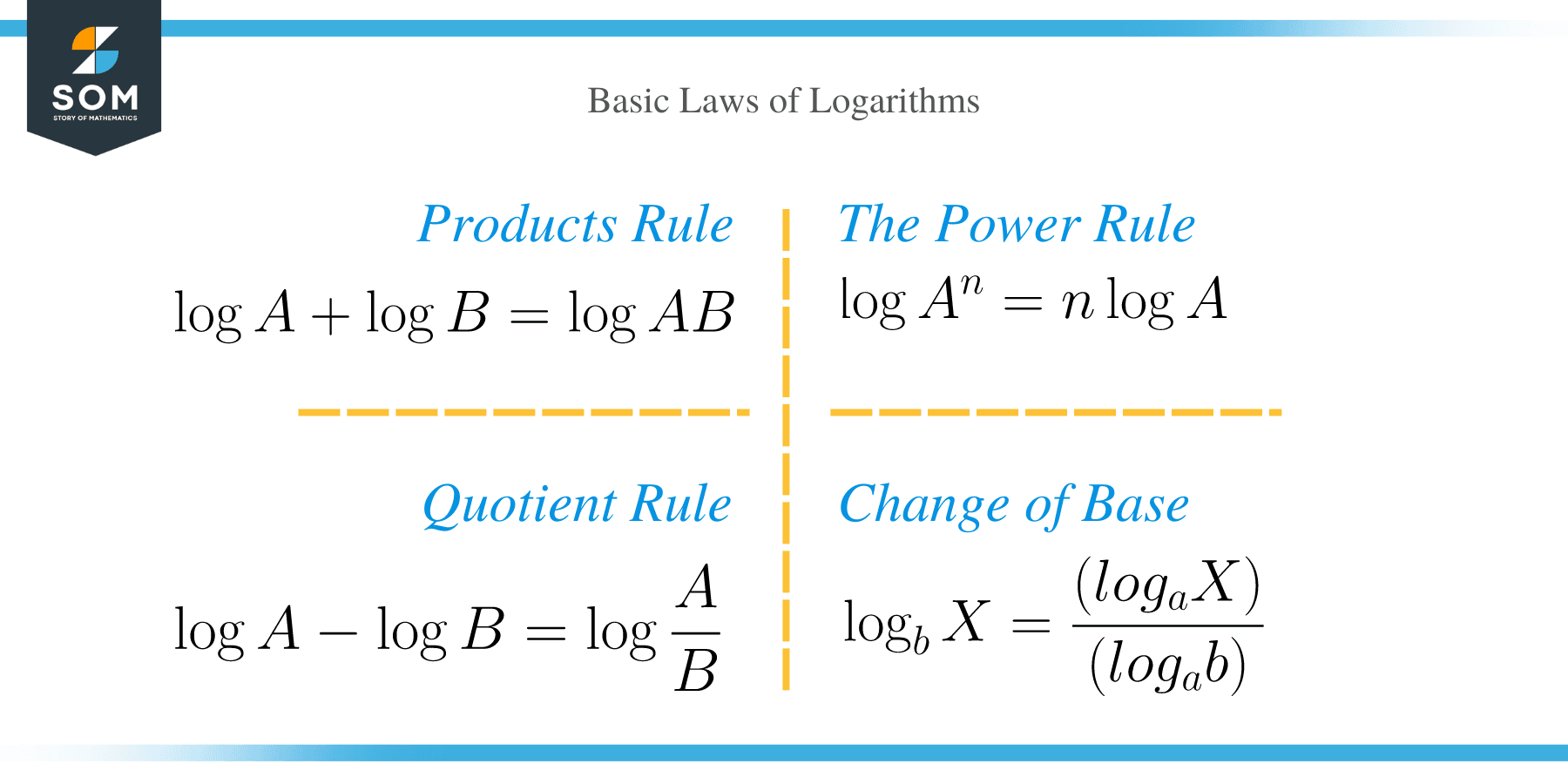
Logarithm Rules Explanation Examples There are mainly 4 important log rules which are stated as follows: the following log rules are derived from the formula of logarithmic form to exponential form and vice versa (b x = m ⇔ log b m = x). along with these rules, we have several other rules of logarithms. all logarithm rules are mentioned below:. This page covers all 8 log rules (including the change of base formula and log exponent rules). each log rule is covered in depth with simple explanations and examples.

Logarithm Rules List Of All The Log Rules With Examples 43 Off

Thank you for being a part of our Logarithm Rules Example journey. Here's to the exciting times ahead!

Properties of Logarithms

Properties of Logarithms

Properties of Logarithms LAWS OF LOGARITHM with solved examples. Lesson 2 Logarithms, Laws of Logs Logarithms, Explained - Steve Kelly Lesson 1 Logarithms, Basics and Properties of Logs Logarithm rules example Rules of Logarithms | Don't Memorise Log rules example 8 in 10 students FAILED this logarithmic equation! Logarithms - The Easy Way! Logs Everything You Need to Know Precalculus - Example Problem - Properties of Logarithms Logarithm Fundamentals | Ep. 6 Lockdown live math 06 - Proving the Logarithm (Log) Rules - Understand Logarithm Rules & Laws of Logs Solving Logarithmic Equations (Hard) Logs and Log Rules Example Learn to use the rules of logarithms to solve a logarithmic equation Natural Logarithms Logarithms Explained: Log Rules & Example Problems | You should know these! Laws of exponents #ajmathematicaltutor

Conclusion

After exploring the topic in depth, one can conclude that write-up provides worthwhile knowledge related to Logarithm Rules Example. From start to finish, the scribe presents extensive knowledge in the domain. Specifically, the section on core concepts stands out as particularly informative. The text comprehensively covers how these features complement one another to build a solid foundation of Logarithm Rules Example.

Furthermore, the piece is remarkable in elucidating complex concepts in an easy-to-understand manner. This simplicity makes the content valuable for both beginners and experts alike. The writer further improves the examination by embedding fitting cases and tangible use cases that place in context the abstract ideas.

Another element that makes this piece exceptional is the thorough investigation of several approaches related to Logarithm Rules Example. By analyzing these diverse angles, the publication gives a balanced perspective of the subject matter. The thoroughness with which the writer tackles the theme is genuinely impressive and sets a high standard for comparable publications in this discipline.

To summarize, this piece not only enlightens the reader about Logarithm Rules Example, but also motivates additional research into this interesting theme. For those who are just starting out or an experienced practitioner, you will uncover worthwhile information in this exhaustive content. Many thanks for taking the time to this detailed post. If you have any questions, you are welcome to reach out via the feedback area. I am excited about your comments. For more information, below are some associated publications that you may find valuable and additional to this content. May you find them engaging!