Logarithms The Easy Way Youtube Can someone please tell me what purposes logarithms have in the everyday world? what non theoretical applications are they in and when would one use them?. I was wondering how one would multiply two logarithms together? say, for example, that i had: $$\\log x·\\log 2x < 0$$ how would one solve this? and if it weren't possible, what would its doma.

Evaluating Logarithms The Easy Way Explained In 2 Minutes Youtube Logarithms are defined as the solutions to exponential equations and so are practically useful in any situation where one needs to solve such equations (such as finding how long it will take for a population to double or for a bank balance to reach a given value with compound interest). historically, they were also useful because of the fact that the logarithm of a product is the sum of the. Seeking an asymptotic formula for the first zeros of a sine sum with logarithmic frequency ∑ summation logarithms asymptotics harmonic functions. As the title states, i need to be able to calculate logs (base $10$) on paper without a calculator. for example, how would i calculate $\\log(25)$?. Logarithm of a quantity really only makes sense if the quantity is dimensionless, and then the result is also a dimensionless number. so what you really plot is not log(y) log (y) but log(y y0) log (y y 0) where y0 y 0 is some reference quantity in the same units as y y (in this case y0 = y 0 = 1 volt). similarly for exp exp and sin sin.

Logarithms The Easy Way Worksheets Library As the title states, i need to be able to calculate logs (base $10$) on paper without a calculator. for example, how would i calculate $\\log(25)$?. Logarithm of a quantity really only makes sense if the quantity is dimensionless, and then the result is also a dimensionless number. so what you really plot is not log(y) log (y) but log(y y0) log (y y 0) where y0 y 0 is some reference quantity in the same units as y y (in this case y0 = y 0 = 1 volt). similarly for exp exp and sin sin. Well, logarithms in general were an useful tool for computing. i guess they came in first. then probably someone saw that we can use ∫x 1 1 tdt ∫ 1 x 1 t d t as an alternative definition of ln(x) ln ⁡ (x). 1 why invent logarithms to do something that exponents already do just fine. exponents do the exact opposite of logarithms, so this question is a non sequitur. I have a very simple question. i am confused about the interpretation of log differences. here a simple example: $$\\log(2) \\log(1)=.3010$$ with my present understanding, i would interpret the resul. Does anyone know a closed form expression for the taylor series of the function f(x) = log(x) f (x) = log (x) where log(x) log (x) denotes the natural logarithm function?.

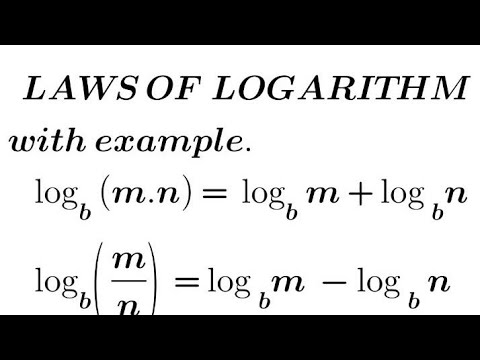
Logarithms Laws With Examples Easy Way Algebra Logarithm Well, logarithms in general were an useful tool for computing. i guess they came in first. then probably someone saw that we can use ∫x 1 1 tdt ∫ 1 x 1 t d t as an alternative definition of ln(x) ln ⁡ (x). 1 why invent logarithms to do something that exponents already do just fine. exponents do the exact opposite of logarithms, so this question is a non sequitur. I have a very simple question. i am confused about the interpretation of log differences. here a simple example: $$\\log(2) \\log(1)=.3010$$ with my present understanding, i would interpret the resul. Does anyone know a closed form expression for the taylor series of the function f(x) = log(x) f (x) = log (x) where log(x) log (x) denotes the natural logarithm function?.

How To Solve For X Using Laws Of Logarithms In A Easy Way Youtube I have a very simple question. i am confused about the interpretation of log differences. here a simple example: $$\\log(2) \\log(1)=.3010$$ with my present understanding, i would interpret the resul. Does anyone know a closed form expression for the taylor series of the function f(x) = log(x) f (x) = log (x) where log(x) log (x) denotes the natural logarithm function?.

A Question On Basic Rules Of Logarithms Easy To Learn This Solution