Python Modulo Using The Operator Real Python What does modulo in the following piece of code do? from math import * 3.14 % 2 * pi how do we calculate modulo on a floating point number?. 0 modulus operator gives you the result in 'reduced residue system'. for example for mod 5 there are 5 integers counted: 0,1,2,3,4. in fact 19=12=5= 2= 9 (mod 7). the main difference that the answer is given by programming languages by 'reduced residue system'.

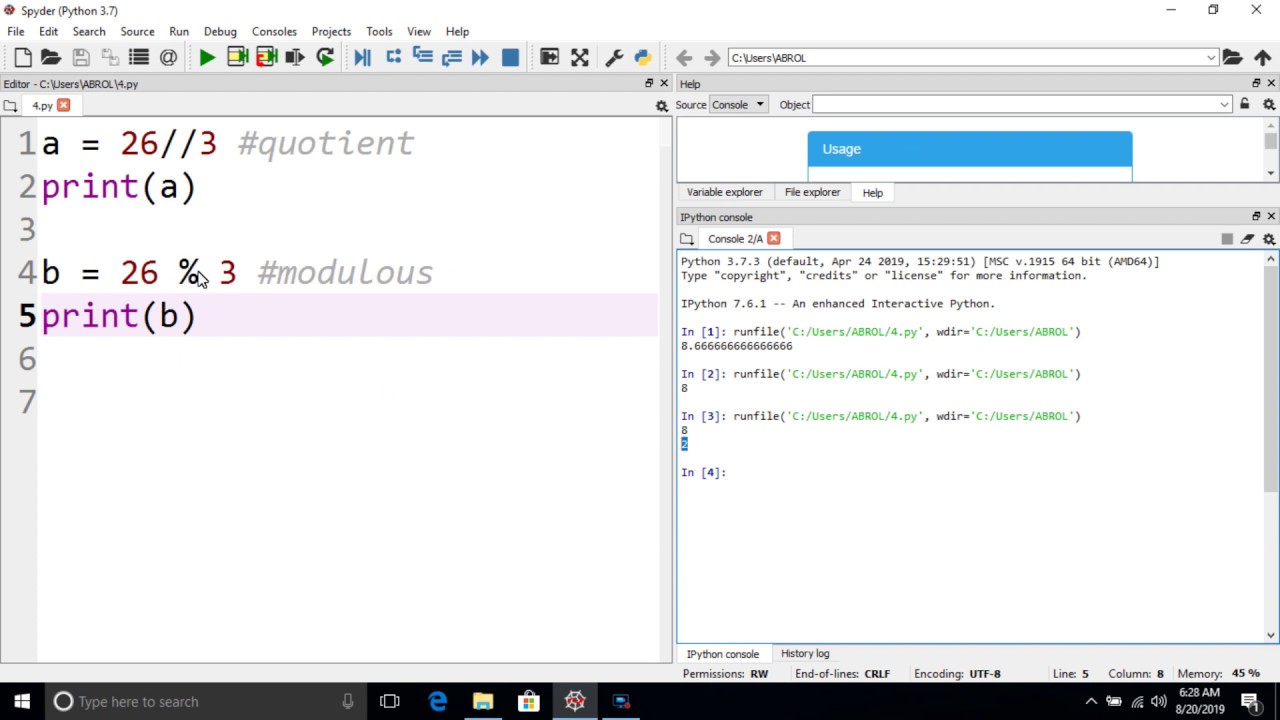
Python Modulo Operator Examples Askpython 44 Off This is because in javascript % is the "remainder" operator while in python it is the "modulus" (clock math) operator. you can get the explanation directly from gvr: edit dahiya boy in java and ios 11 % 5 = 1 whereas in python and ruby 11 % 5 = 4. well half of the reason is explained by the paulo scardine, and rest of the explanation is. I am new to programming, and i chose to learn python, and i came across this operator (%) called modulus, but i don't understand it, can some explain it to me in more detail!. Division and modulo are both o (n^2) algorithms in python. dividing a 2000 digit number by a 1000 digit number will take about 4 times longer than dividing a 1000 digit number by a 500 digit number. the ratio will become closer to 4 if you keep doubling the number of digits. Open up the python console, and do 4 % 2, what is the result? then do 3 % 2, what is the result? now which of the results would be considered "true"? the modulo operator returns the remainder after a division. if the division is even (like in 4 % 2) then there is no remainder, the result is 0.

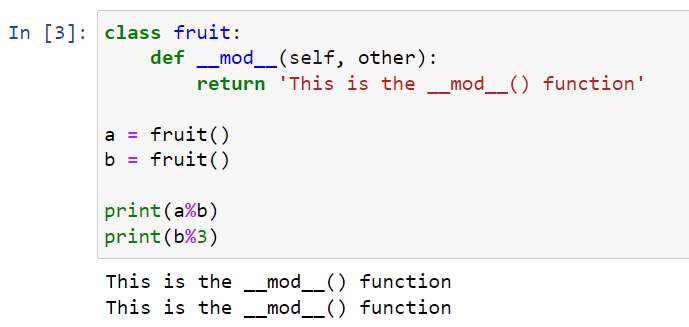
Python Modulo Operator Examples Askpython 44 Off Division and modulo are both o (n^2) algorithms in python. dividing a 2000 digit number by a 1000 digit number will take about 4 times longer than dividing a 1000 digit number by a 500 digit number. the ratio will become closer to 4 if you keep doubling the number of digits. Open up the python console, and do 4 % 2, what is the result? then do 3 % 2, what is the result? now which of the results would be considered "true"? the modulo operator returns the remainder after a division. if the division is even (like in 4 % 2) then there is no remainder, the result is 0. Python has a "true" modulo operation, while c has a remainder operation. it has a direct relation with how the negative integer division is handled, i.e. rounded towards 0 or minus infinite. python rounds towards minus infinite and c (99) towards 0, but in both languages (n m)*m n%m == n, so the % operator must compensate in the correct. Exactly how does the % operator work in python, particularly when negative numbers are involved? for example, why does 5 % 4 evaluate to 3, rather than, say, 1?. Note that the modulo operator always returns a positive number, so for negative numbers it might not be what you would expect when talking about the remainder: 10 % 3 == 2. however a b*b a%b == a still holds true, since python always rounds towards infinity, unlike some other languages, which round towards 0 but would return 1. For large integers, python division (and modulo) use an o (n^2) algorithm. multiplication uses the karatsuba multiplication which is o (n^1.585) but division uses basic "grade school" division.

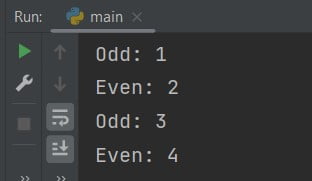
Python Modulo Operator Python has a "true" modulo operation, while c has a remainder operation. it has a direct relation with how the negative integer division is handled, i.e. rounded towards 0 or minus infinite. python rounds towards minus infinite and c (99) towards 0, but in both languages (n m)*m n%m == n, so the % operator must compensate in the correct. Exactly how does the % operator work in python, particularly when negative numbers are involved? for example, why does 5 % 4 evaluate to 3, rather than, say, 1?. Note that the modulo operator always returns a positive number, so for negative numbers it might not be what you would expect when talking about the remainder: 10 % 3 == 2. however a b*b a%b == a still holds true, since python always rounds towards infinity, unlike some other languages, which round towards 0 but would return 1. For large integers, python division (and modulo) use an o (n^2) algorithm. multiplication uses the karatsuba multiplication which is o (n^1.585) but division uses basic "grade school" division.