Ppt Floating Point Computer Architecture And Organization Powerpoint Specifically a 64 bit floating point number relating to the horizontal velocity of the rocket with respect to the platform was converted to a 16 bit signed integer. We often incur floating point programming. we’ll focus on the ieee 754 standard for floating point arithmetic. ieee numbers are stored using a kind of scientific notation. we can represent floating point numbers with three binary fields: a sign bit s, an exponent field e, and a fraction field f.

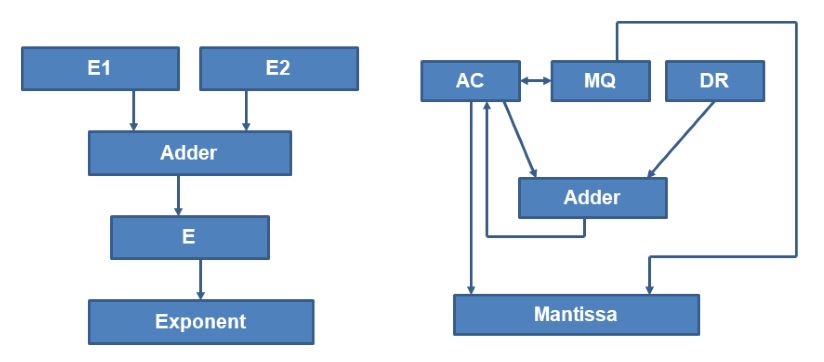
Floating Point Arithmetic Computer Architecture To understand how to represent floating point numbers in the computer and how to perform arithmetic with them. also to learn how to use floating point arithmetic in mips. Moving floating point data can be done using the standard mov instruction in assembly language. if the source and destination are different length, care must be taken in conversion to ensure that exponent and significand are properly converted. underflow – a magnitude too small to represent as an integer. Floating point numbers allow very large and very small numbers to be represented using only a few digits, at the expense of precision. the precision is primarily determined by the number of digits in the fraction (or significand, which has integer and fractional parts), and the range. Floating point multiplication algorithm input: two single precision, floating point numbers x, and y output: x * y.

Solution Computer Organization And Architecture Floating Point Floating point numbers allow very large and very small numbers to be represented using only a few digits, at the expense of precision. the precision is primarily determined by the number of digits in the fraction (or significand, which has integer and fractional parts), and the range. Floating point multiplication algorithm input: two single precision, floating point numbers x, and y output: x * y. Question: coe 224: computer organization and architecture ! lab 5: floating point arithmetic objectives • to learn and practice the floating point arithmetic of mips instruction set. requirements: a desktop or laptop computer. download the spim simulator (qtspim). Ieee floating point representation • the mantissa is the set of 0’s and 1’s to the right of the radix point of the normalized (when the digit to the left of the radix point is 1) binary number. Chapter 1 provides a general introduction to computer architecture, and then proposes the notion of an instruction set architecture. we ponder on the question of completeness of an isa by taking recourse to results developed by the founder of computer science, alan turing. Floating point representation solves this problem. floating point numbers allow an arbitrary number of decimal places to the right of the decimal point. they are often expressed in scientific notation. which is the standard arrangement of these fields.

Co And Architecture Computer Organization Floating Point Representation Question: coe 224: computer organization and architecture ! lab 5: floating point arithmetic objectives • to learn and practice the floating point arithmetic of mips instruction set. requirements: a desktop or laptop computer. download the spim simulator (qtspim). Ieee floating point representation • the mantissa is the set of 0’s and 1’s to the right of the radix point of the normalized (when the digit to the left of the radix point is 1) binary number. Chapter 1 provides a general introduction to computer architecture, and then proposes the notion of an instruction set architecture. we ponder on the question of completeness of an isa by taking recourse to results developed by the founder of computer science, alan turing. Floating point representation solves this problem. floating point numbers allow an arbitrary number of decimal places to the right of the decimal point. they are often expressed in scientific notation. which is the standard arrangement of these fields.