Solved Let G Be A Group And Set Diag G G G I G E G C Chegg There’s just one step to solve this. let g be a set of rational numbers other than 1. let * be an operation on g defined by a*b=a b a not the question you’re looking for? post any question and get expert help quickly. Ation law to derive these implications. it follows that b = ba for all choices of a an 13: we start with some general remarks. let g be a group and let e denote the identity element of g. we have ea = a and ae = a for all a ∈ g. thus, ea = ae for all a ∈ g. furtherm re, sup ab = e =⇒ ab = aa−1 =⇒ b = a−1 =⇒ ba = a−1a = e .

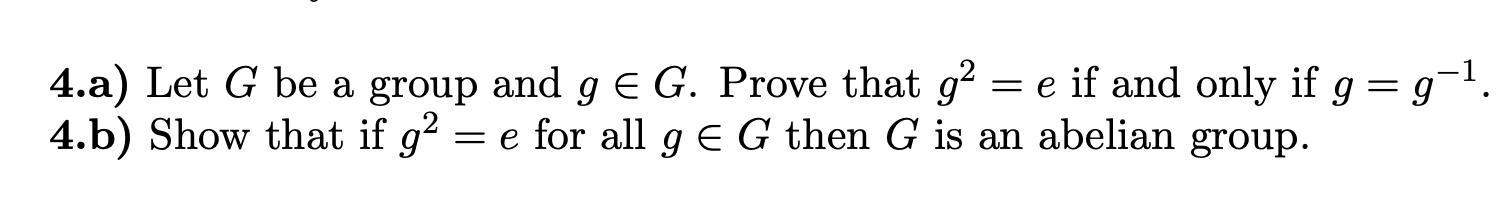
Solved 4 A Let G Be A Group And Gв G Prove That G2 E If And Chegg Let g be a group and let g0 = haba 1b 1i; that is, g0 is the subgroup of all nite products of elements in g of the form aba 1b 1. the subgroup g0 is called the commutator subgroup of g. Let g be a group, and a, b, c be elements of g. if a b = a c, show that b = c. in a group g, given that ab = ac, we can prove b = c using the properties of a group. multiply both sides of the equation by a⁻¹ from the left: (a⁻¹ * a) * b = (a⁻¹ * a) * c. then, using the identity element, we get e * b = e * c, which simplifies to b = c. Problem 1. let g be a group. prove that if a ∈ g has finite order n then, for any integer k, the. rder of ak is n gcd(n, k). suppose that a ∈ g has ord. r m and b ∈ g has order n. supp. se furthermore that ab = ba. prove that the order. of ab divides mn gcd(m, n). prove that both m gcd(m, n) and n gcd(m, n) divide the order of ab. Let $g$ be a group, and let $g \in g$. let $\varphi g : g \to g $ be defined by $\varphi g (x) = gx$ for $x \in g$. for which $g \in g$ is $\varphi g$ a homomorphism? i solved this below let $x , y.

Solved Let G Be A Group And Hтйдg A Prove For Any Chegg Problem 1. let g be a group. prove that if a ∈ g has finite order n then, for any integer k, the. rder of ak is n gcd(n, k). suppose that a ∈ g has ord. r m and b ∈ g has order n. supp. se furthermore that ab = ba. prove that the order. of ab divides mn gcd(m, n). prove that both m gcd(m, n) and n gcd(m, n) divide the order of ab. Let $g$ be a group, and let $g \in g$. let $\varphi g : g \to g $ be defined by $\varphi g (x) = gx$ for $x \in g$. for which $g \in g$ is $\varphi g$ a homomorphism? i solved this below let $x , y. Let g be a group and c be a fixed element of g. define a new operation * on g by x ∗ y = x c 1 y for all x and y in g. prove that g is a group under the operation ∗. 1, let g be a group containing 4 elements a, b, c, and d. under the group operation called the multiplication, we know that ab = d and c2 = d. which element is b2? how about bc? justify your answer. 2. let g = {a, b, c, d, e} be a set with an associative binary operation multiplication such that ab = ba = d, ed = de = c. prove that g under. There’s just one step to solve this. let us assume that d = gcd (k, l, n) . then, k = d k ′, l = d l ′, n = d n ′ . (a d) k ′ = a k, (a d) l ′ = a l ⇒ a k, a l ∈⇒⊆ … (i) let (g,⋅) be a group and let a∈g be an element of order ∣a∣=n<∞. prove that ak,al = agcd(k,l,n) . not the question you’re looking for?. Question: 4. (4.5.23) let g be a group with a,b∈g. prove: (a) the order of a is the same as the order of a−1. (b) for all g∈g,∣a∣=∣∣g−1ag∣∣. (c) the order of ab is the same as the order of ba. show transcribed image text.

Solved 4 Let G Be A Group And Let N Be A Normal Subgroup Of Chegg Let g be a group and c be a fixed element of g. define a new operation * on g by x ∗ y = x c 1 y for all x and y in g. prove that g is a group under the operation ∗. 1, let g be a group containing 4 elements a, b, c, and d. under the group operation called the multiplication, we know that ab = d and c2 = d. which element is b2? how about bc? justify your answer. 2. let g = {a, b, c, d, e} be a set with an associative binary operation multiplication such that ab = ba = d, ed = de = c. prove that g under. There’s just one step to solve this. let us assume that d = gcd (k, l, n) . then, k = d k ′, l = d l ′, n = d n ′ . (a d) k ′ = a k, (a d) l ′ = a l ⇒ a k, a l ∈⇒⊆ … (i) let (g,⋅) be a group and let a∈g be an element of order ∣a∣=n<∞. prove that ak,al = agcd(k,l,n) . not the question you’re looking for?. Question: 4. (4.5.23) let g be a group with a,b∈g. prove: (a) the order of a is the same as the order of a−1. (b) for all g∈g,∣a∣=∣∣g−1ag∣∣. (c) the order of ab is the same as the order of ba. show transcribed image text.

Solved 12 Let G Be A Group And Let D A A в јaв G A Prove Chegg There’s just one step to solve this. let us assume that d = gcd (k, l, n) . then, k = d k ′, l = d l ′, n = d n ′ . (a d) k ′ = a k, (a d) l ′ = a l ⇒ a k, a l ∈⇒⊆ … (i) let (g,⋅) be a group and let a∈g be an element of order ∣a∣=n<∞. prove that ak,al = agcd(k,l,n) . not the question you’re looking for?. Question: 4. (4.5.23) let g be a group with a,b∈g. prove: (a) the order of a is the same as the order of a−1. (b) for all g∈g,∣a∣=∣∣g−1ag∣∣. (c) the order of ab is the same as the order of ba. show transcribed image text.