Solved 50 Chapter 1 Group Representations 8 Let V Be A Chegg

Solved 50 Chapter 1 Group Representations 8 Let V Be A Chegg Show that the following properties will hold in v if and only if a related property holds for a basis of v. (a) v is a g module. (b) the map 0: vw is a g homomorphism. 2. groups let v be a vector space over the eld f . the set of all linear in vertible maps from v to v is called general linear group of v and denoted by gl(v ). 2.1. suppose that f is a nite eld with say jf j = pm = q and that v has nite dimension n over f . then nd the order of gl(v ).

Solved 8 Let G Be A Group And H Chegg Theorem 1.6.5 (schur's lemma) let v and w be two irreducible g. modules. if : vw is a g homomorphism, then either. 1.0 is a g isomorphism, or 2.0 is the zero map. At chegg we understand how frustrating it can be when you’re stuck on homework questions, and we’re here to help. our extensive question and answer board features hundreds of experts waiting to provide answers to your questions, no matter what the subject. Search our library of 100m curated solutions that break down your toughest questions. ask one of our real, verified subject matter experts for extra support on complex concepts. test your knowledge anytime with practice questions. create flashcards from your questions to quiz yourself. Theorem: let g g be a abelian group and (v, ρ) (v, ρ) be a irreducible representation of g g over a algebraically closed field k k. if v v is finite dimensional (more generally, if dimkv <|k|) d i m k v <| k |) then dimkv = 1 d i m k v = 1.

Solved 25 Problem 1 Let G Be A Group And Let A B E G Chegg Search our library of 100m curated solutions that break down your toughest questions. ask one of our real, verified subject matter experts for extra support on complex concepts. test your knowledge anytime with practice questions. create flashcards from your questions to quiz yourself. Theorem: let g g be a abelian group and (v, ρ) (v, ρ) be a irreducible representation of g g over a algebraically closed field k k. if v v is finite dimensional (more generally, if dimkv <|k|) d i m k v <| k |) then dimkv = 1 d i m k v = 1. Uppose x = v is a vector space. then we can say that g a (c) g(u v) = gu gv, (d) g(rv) = r(gv). each representation a of g in v defines a linear action of g on v , by gv = a(g)v; and every such action arises from a representation in this way. ion are completely equiv alent. we can use whichever we find or. 2 the group z admits a continuous series of 1 dimensional unitary representations dμ, with μ 2 [0; 21⁄4], given by dμ(n) = einμ ; (1.1.67) where μ labels the representation, while n is the group element of z. Math 594. solutions to exam 1 1. (20 pts) let gbe a group. we de ne its automorphism group aut(g) to be the set of group isomorphisms ˚: g’g. (i) (5 pts) prove that using composition of maps, aut(g) is a group. (ii) (5 pts) for g2g, de ne c g: g’gto be the left conjugation action: c g(g0) = gg0g1. prove that c g2aut(g) and that g7!c. Let be an irreducible complex representation of the finite group g on v . then the isotypical component of the representation c[g] corresponding to contains exactly dim v times.

Solved Chapter 8 Section 8 1 Question 31 Let V1 V2 And Chegg Uppose x = v is a vector space. then we can say that g a (c) g(u v) = gu gv, (d) g(rv) = r(gv). each representation a of g in v defines a linear action of g on v , by gv = a(g)v; and every such action arises from a representation in this way. ion are completely equiv alent. we can use whichever we find or. 2 the group z admits a continuous series of 1 dimensional unitary representations dμ, with μ 2 [0; 21⁄4], given by dμ(n) = einμ ; (1.1.67) where μ labels the representation, while n is the group element of z. Math 594. solutions to exam 1 1. (20 pts) let gbe a group. we de ne its automorphism group aut(g) to be the set of group isomorphisms ˚: g’g. (i) (5 pts) prove that using composition of maps, aut(g) is a group. (ii) (5 pts) for g2g, de ne c g: g’gto be the left conjugation action: c g(g0) = gg0g1. prove that c g2aut(g) and that g7!c. Let be an irreducible complex representation of the finite group g on v . then the isotypical component of the representation c[g] corresponding to contains exactly dim v times.

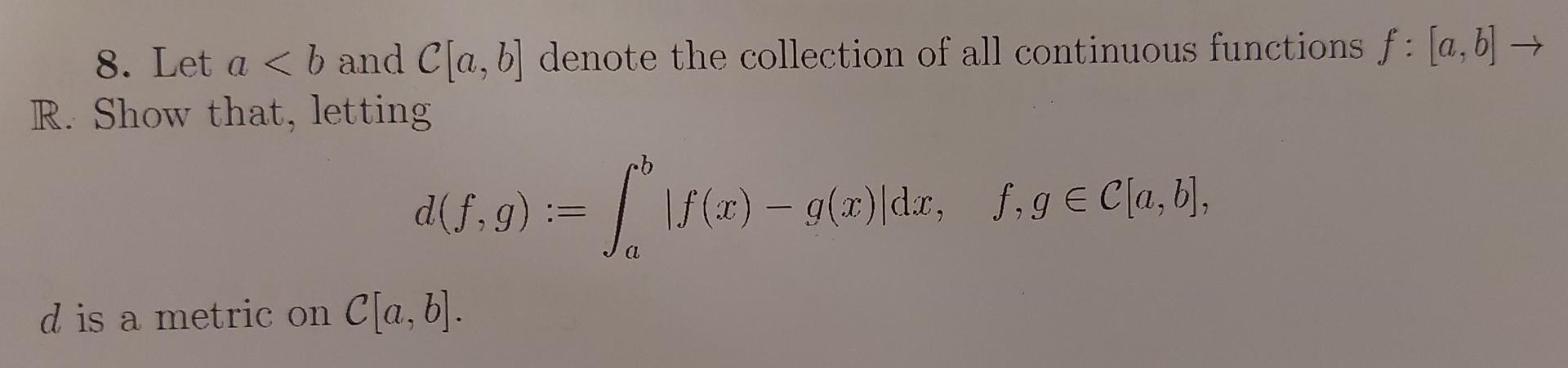
Solved 8 Let A Chegg Math 594. solutions to exam 1 1. (20 pts) let gbe a group. we de ne its automorphism group aut(g) to be the set of group isomorphisms ˚: g’g. (i) (5 pts) prove that using composition of maps, aut(g) is a group. (ii) (5 pts) for g2g, de ne c g: g’gto be the left conjugation action: c g(g0) = gg0g1. prove that c g2aut(g) and that g7!c. Let be an irreducible complex representation of the finite group g on v . then the isotypical component of the representation c[g] corresponding to contains exactly dim v times.

Step into a world where your Solved 50 Chapter 1 Group Representations 8 Let V Be A Chegg passion takes center stage. We're thrilled to have you here with us, ready to embark on a remarkable adventure of discovery and delight.

Lecture 6

Lecture 6

Lecture 6 Tensor Tutorial part 1 of 6 - Groups and Representations Lecture 8 Representation Theory 28 Discrete Representation Theory Ep. 8 - Reducibility Lie Groups and Lie Algebras: Lesson 41: Elementary Representation Theory I Algebraic Representation Representation theory: Examples D8, A4, S4, S5, A5 Representation theory: Introduction Gerhard Hiss: Representation theory for groups of Lie type II Mathematical Structure of Quantum Theory Lecture 3: Representation Theory for Quantum Mechanics MA538 Representation theory of finite groups Lecture1B RT1: Representation Theory Basics Representation theory of finite groups. Lecture 14: Specht modules (by Walter Mazorchuk) [Lie Groups and Lie Algebras] Lecture 5. Basic representation theory Lie groups and Lie algebras: New representations from old Discrete Representation Theory Ep. 10 - Group Algebras Discrete Representation Theory Ep. 11 - The Regular FG-Module (Regular Representations) Lecture 8, MTH 204A (Section B) Representation theory of finite groups. Lecture 12: problem session (by Walter Mazorchuk)

Conclusion

Considering all the aspects, it is clear that article shares worthwhile information on Solved 50 Chapter 1 Group Representations 8 Let V Be A Chegg. In the entirety of the article, the content creator illustrates considerable expertise in the domain. Markedly, the portion covering fundamental principles stands out as a crucial point. The presentation methodically addresses how these features complement one another to provide a holistic view of Solved 50 Chapter 1 Group Representations 8 Let V Be A Chegg.

Moreover, the publication excels in disentangling complex concepts in an user-friendly manner. This simplicity makes the content beneficial regardless of prior expertise. The writer further augments the discussion by including relevant scenarios and actual implementations that help contextualize the intellectual principles.

A supplementary feature that makes this post stand out is the exhaustive study of different viewpoints related to Solved 50 Chapter 1 Group Representations 8 Let V Be A Chegg. By considering these various perspectives, the publication offers a well-rounded view of the matter. The completeness with which the content producer handles the issue is extremely laudable and raises the bar for comparable publications in this subject.

In conclusion, this piece not only educates the viewer about Solved 50 Chapter 1 Group Representations 8 Let V Be A Chegg, but also inspires continued study into this interesting topic. If you happen to be a beginner or a seasoned expert, you will encounter useful content in this thorough article. Thank you sincerely for engaging with this comprehensive article. If you need further information, please do not hesitate to reach out through our messaging system. I am excited about hearing from you. For further exploration, below are a few relevant pieces of content that are helpful and complementary to this discussion. May you find them engaging!