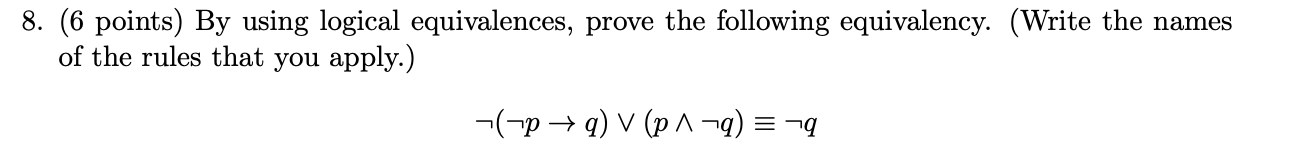
Solved 8 6 Points By Using Logical Equivalences Prove Chegg There are 4 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. What does it mean for two logical statements to be the same? in this section, we’ll meet the idea of logical equivalence and visit two methods to show two statements are equivalent.

Solved 6 ï Points ï By Using Logical Equivalences Prove The Chegg Exercise 1: use truth tables to show that ~ ~p o p (the double negation law) is valid. exercise 2: use truth tables to show that p Ù t o p (an identity law) is valid. note: any equivalence termed a “law” will be proven by truth table, but all others by proof (as we shall see next). By using inference rules, we can prove the conclusion follows from the premises. in inference, we can always replace a logic formula with another one that is logically equivalent, just as we have seen for the implication rule. Certainly, if a rst expression is equivalent to a second, and a second is equivalent to a third, then the rst is equivalent to the third. this is known as transitivity. A simple and straightforward approach is to construct truth tables if you have a few primitive statements or logical variables.

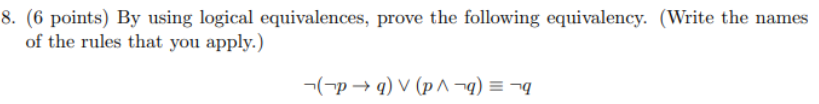
Solved 8 6 Points By Using Logical Equivalences Prove Chegg Certainly, if a rst expression is equivalent to a second, and a second is equivalent to a third, then the rst is equivalent to the third. this is known as transitivity. A simple and straightforward approach is to construct truth tables if you have a few primitive statements or logical variables. Question: 1. (6 points) show the logical equivalences using truth tables and say a few words explaining why your truth table shows ≡ (a) ¬ (p∨q)≡¬p∧¬q (demorgan's law). What are logical equivalences and why are they useful? definition: compound propositions p and q are logically equivalent exactly when p q is a tautology. the notation p q means that p and q are logically equivalent. logical equivalences are extremely useful!. Sometimes using truth tables to prove logical equivalences can be very tedious. in these cases, a more efficient method is to use the table of logical equivalences that you have been provided with. Prove that the following two expressions are logically equivalent. use truth tables, logical laws, or natural deduction as necessary. show each step clearly:.