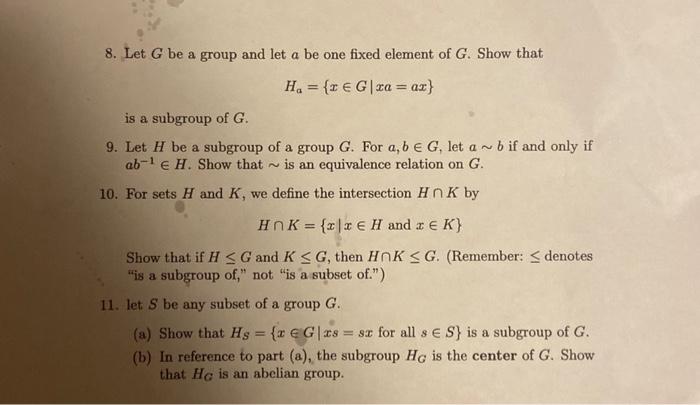
Solved 8 Let G Be A Group And Let A Be One Fixed Element Of Chegg Let s be any subset of a group g. (a) show that h s ={x∈g∣xs= sx for all s∈s} is a subgroup of g. (b) in reference to part (a), the subgroup h g is the center of g. show that h c is an abelian group. The set ha = {x ∈ g | xa = ax} for a fixed element a in a group g contains all elements of g that commute with a and is a subset of g, making ha a legitimate set in the context of group theory.

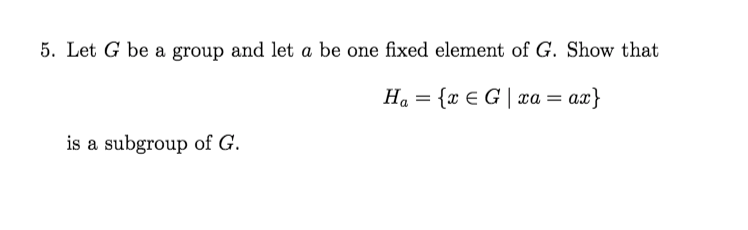
Solved 5 Let G Be A Group And Let A Be One Fixed Element Of Chegg To show that a set is a subgroup of a group, we need to verify three criteria: (1) the identity element of the group is in the set, (2) the set is closed under the group operation, and (3) each element of the set has an inverse in the set. First, we need to show that the identity element e of g is in h a. since a is an element of g, we have e a = a = a e, so e ∈ h a. 2. next, we need to show that if x y ∈ h a, then x y ∈ h a. if x y ∈ h a, then we have x a = a x and y a = a y. we want to show that x y a = a x y. Find step by step solutions and your answer to the following textbook question: let g be a group and let a be one fixed element of g. show that $$ h a = \ { x ∈ g| xa = ax\} $$ is a subgroup of g. G → gx g → g x. 1) injection: assume gx = gy g x = g y. then we premultiply by g−1 g 1 to conclude x = y x = y. 2) onto: let w ∈ g w ∈ g . then g(g−1w) = (gg−1)w = w g (g 1 w) = (g g 1) w = w. so the map x → gx x → g x is a bijection onto g g, so that g g = {gx: x ∈ g g x: x ∈ g} (though showing the map is onto is enough).

Solved Let G Be A Group And Let A Be The Fixed Element Of G Chegg Find step by step solutions and your answer to the following textbook question: let g be a group and let a be one fixed element of g. show that $$ h a = \ { x ∈ g| xa = ax\} $$ is a subgroup of g. G → gx g → g x. 1) injection: assume gx = gy g x = g y. then we premultiply by g−1 g 1 to conclude x = y x = y. 2) onto: let w ∈ g w ∈ g . then g(g−1w) = (gg−1)w = w g (g 1 w) = (g g 1) w = w. so the map x → gx x → g x is a bijection onto g g, so that g g = {gx: x ∈ g g x: x ∈ g} (though showing the map is onto is enough). Let g be a group and let a be a fixed element of g. show that the map lambda a:gto g , given by lambda a (g)=ga^ ( 1) for g∈ g , is a permutation of the set g. A (x − 1) = x − 1 (x a − 1). thus, (x − 1) a = a (x − 1), and so x − 1 ∈ h a. since h a contains the identity element, is closed under the group operation, and contains the inverse of each of its elements, we can conclude that h a is a subgroup of g. Solution for let g be a group and let a be a fixed element of g. show that the map λ0 :g→g, given by λa (g)=ag for g∈g, is a permutation of the set g. Math algebra algebra questions and answers let g be a group and let a be one fixed element of g. show that ha = {x ∈ g | xa = ax} is a subgroup of g.