Solved Chegg Chegg Chegg Chegg Chegg Chegg Chegg Chegg Chegg Chegg Show the following equivalences using using logical equivalence laws. (a) (p→r)∨ (q→r)≡ (p∧q)→r (b) p∧ (q∨r)≡ (p∧q)∨ (p∧r). (c) ¬ [¬ [ (p∨q)∧r]∨¬q]≡q∧r (d) (p∨q∨r)∧ (p∨t∨¬q)∧ (p∨¬t∨r)≡p∨ [r∧ (t∨¬q)] your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: 8. Show the following equivalence using both truth tables and the laws of logic. in your laws of logic solution, justify each of your steps by stating which law you are using.

Solved 8 Show The Following Equivalences Using Using Chegg Exercise 1.8.1: applying de morgan's law for quantified statements to logical expressions. apply de morgan's law to each expression to obtain an equivalent expression in which each negation sign applies directly to a predicate. Equivalently, we want to show the following proposition is t (the domain for n ;x;y;z is all positive integers.) 8 (n 3 ):9 x 9 y 9 z (xn yn= zn) this problem had been open for more than 350 years. Using the inference rules above, we can solve the following riddle by first formalizing the text into propositional logic and then using the inference rules to find the glasses. We need eight combinations of truth values in p p, q q, and r r. we list the truth values according to the following convention. in the first column for the truth values of p p, fill the upper half with t and the lower half with f.

Solved 6 Show The Following Equivalences Either Using Venn Chegg Using the inference rules above, we can solve the following riddle by first formalizing the text into propositional logic and then using the inference rules to find the glasses. We need eight combinations of truth values in p p, q q, and r r. we list the truth values according to the following convention. in the first column for the truth values of p p, fill the upper half with t and the lower half with f. The following table is a set of core tautologies we will be using for the rest of the course. in the example that follows them, we will show how we can use these existing tautologies (which we’ll call laws) to make conclusions about more complex statements. Determine whether the two expressions are logically equivalent, that is, for each interpre tation they lead to the same value. hint: use truth table to show the equivalence. Often used to mean statements r and s are logically equivalent is r s. you can determine whether compound propositions r and s are logically equivalent by building a single truth table for both propos. tions and checking to see that they have exactly the same truth values. notice the new symbol r , s, which is used to denote that r and s are log. Click and drag the steps in the correct order to show that ¬p → (q → r) and q → (p ∨ r) are logically equivalent. (note: while proving, prove the equivalence from ¬p → (q → r) to q → (p ∨ r).).

Solved Show The Following Equivalences Using Logical Chegg The following table is a set of core tautologies we will be using for the rest of the course. in the example that follows them, we will show how we can use these existing tautologies (which we’ll call laws) to make conclusions about more complex statements. Determine whether the two expressions are logically equivalent, that is, for each interpre tation they lead to the same value. hint: use truth table to show the equivalence. Often used to mean statements r and s are logically equivalent is r s. you can determine whether compound propositions r and s are logically equivalent by building a single truth table for both propos. tions and checking to see that they have exactly the same truth values. notice the new symbol r , s, which is used to denote that r and s are log. Click and drag the steps in the correct order to show that ¬p → (q → r) and q → (p ∨ r) are logically equivalent. (note: while proving, prove the equivalence from ¬p → (q → r) to q → (p ∨ r).).

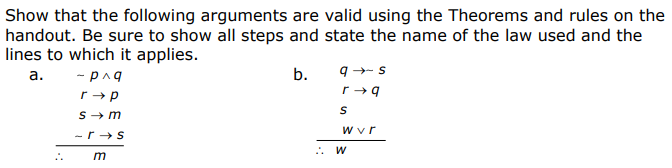
Solved Show The Following Equivalences Using Logical Chegg Often used to mean statements r and s are logically equivalent is r s. you can determine whether compound propositions r and s are logically equivalent by building a single truth table for both propos. tions and checking to see that they have exactly the same truth values. notice the new symbol r , s, which is used to denote that r and s are log. Click and drag the steps in the correct order to show that ¬p → (q → r) and q → (p ∨ r) are logically equivalent. (note: while proving, prove the equivalence from ¬p → (q → r) to q → (p ∨ r).).

Solved Using The Table Of Equivalences From Lectures Show Chegg