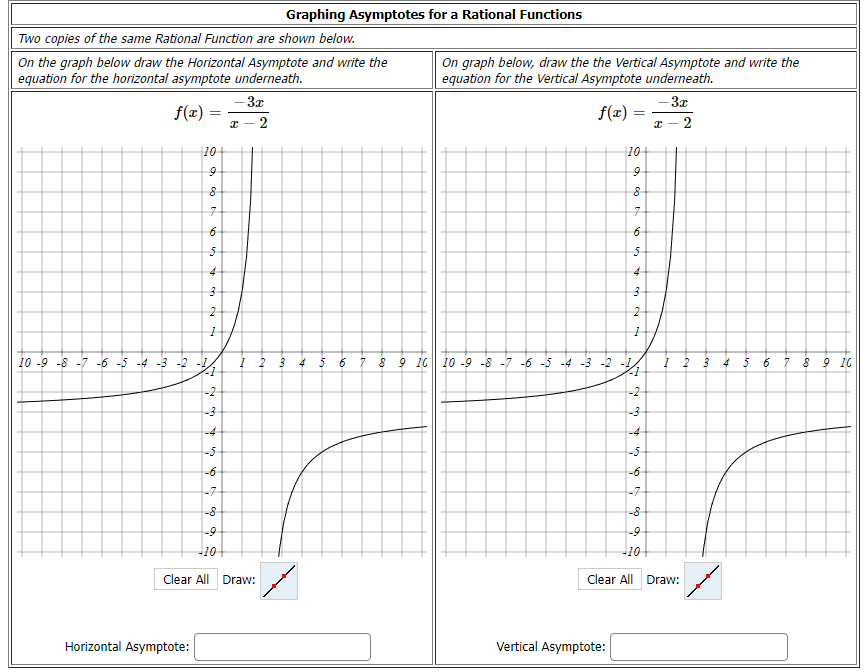
Solved Graphing Asymptotes For A Rational Functions Chegg There are 3 steps to solve this one. given is the rational function f (x) = − 3 x x − 2 . the objective is to draw its horizontal anf vertical asymptote. not the question you’re looking for? post any question and get expert help quickly. By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. we may even be able to approximate their location.

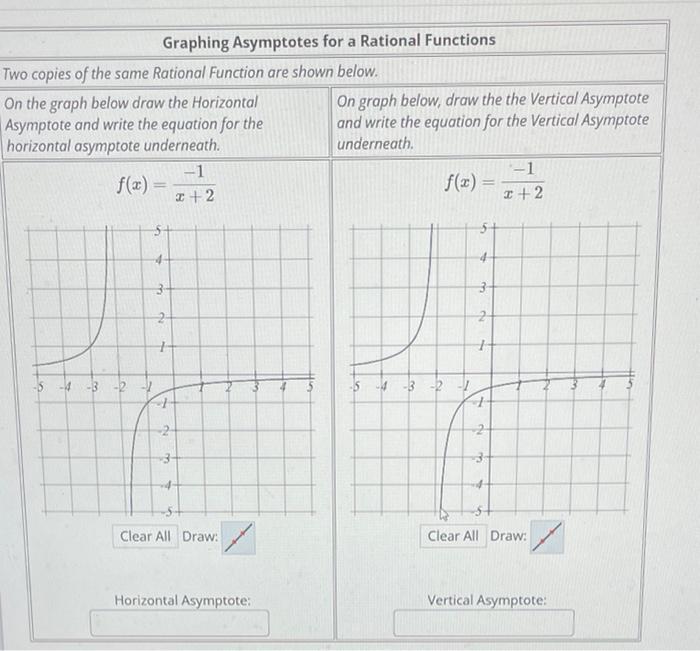
Solved Graphing Asymptotes For A Rational Functions Two Chegg Learn how to find removable discontinuities, horizontal asymptotes, and vertical asymptotes of rational functions. this video explores the specific example f (x)= (3x^2 18x 81) (6x^2 54) before generalizing findings to all rational functions. don't forget that not every zero of the denominator is a vertical asymptote!. Recall from section 1.2 that an even function is symmetric with respect to the y axis, and an odd function is symmetric with respect to the origin. this can sometimes save time in graphing rational functions. Determine if the graph will intersect its horizontal or slant asymptote. if there is a horizontal asymptote, say y=p, then set the rational function equal to p and solve for x. In this section we will discuss a process for graphing rational functions. we will also introduce the ideas of vertical and horizontal asymptotes as well as how to determine if the graph of a rational function will have them.

Solved Graphing Asymptotes For A Rational Functions Submit Chegg Determine if the graph will intersect its horizontal or slant asymptote. if there is a horizontal asymptote, say y=p, then set the rational function equal to p and solve for x. In this section we will discuss a process for graphing rational functions. we will also introduce the ideas of vertical and horizontal asymptotes as well as how to determine if the graph of a rational function will have them. In this section, we explore rational functions, which have variables in the denominator. we have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. examine these graphs, as shown in figure 1, and notice some of their features. Identify the points of discontinuity, holes, vertical sketch the graph. and horizontal asymptote of each. then . discontinuities: , vertical asym.: x holes: x horz. asym.: none. discontinuities: , vertical asym.: x , x holes: none horz. asym.: none. create your own worksheets like this one with infinite algebra 2. Given a rational function (that is, a polynomial fraction) to graph, follow these steps: set the denominator equal to zero, and solve. the resulting values (if any) tell you where the vertical asymptotes are. check the degrees of the polynomials for the numerator and denominator. How to: given a rational function, sketch a graph. evaluate the function at 0 to find the y intercept. factor the numerator and denominator. for factors in the numerator not common to the denominator, determine where each factor of the numerator is zero to find the x x intercepts.