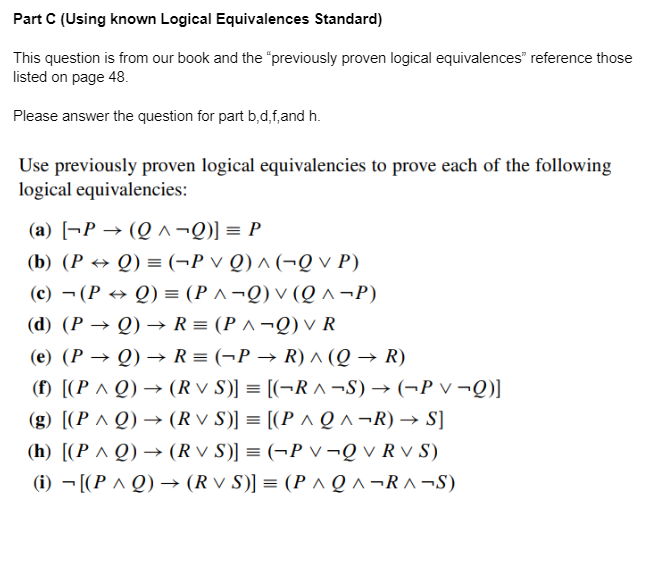
Solved Part C Using Known Logical Equivalences Standard Chegg Part c (using known logical equivalences standard) this question is from our book and the "previously proven logical equivalences" reference those listed on page 48 . please answer the question for part b,d,f, and h. We can use the properties of logical equivalence to show that this compound statement is logically equivalent to t t. this kind of proof is usually more difficult to follow, so it is a good idea to supply the explanation in each step.

Solved Part C Using Known Logical Equivalences Standard Chegg What does it mean for two logical statements to be the same? in this section, we’ll meet the idea of logical equivalence and visit two methods to show two statements are equivalent. In arithmetic, we learn that addition and multiplication are both commutative and associative, and that multiplication distributes over addition. the commutativity of addition means that we can add quantities to each other in di erent orders and get the same result. for example, 1 2 = 3 1. We demonstrated that a → (b → c) is logically equivalent to (a∧b) → c using logical equivalences and properties of implication. by rewriting the implications and using de morgan's laws, we simplified the expressions and established the equivalence. What are logical equivalences and why are they useful? definition: compound propositions p and q are logically equivalent exactly when p q is a tautology. the notation p q means that p and q are logically equivalent. logical equivalences are extremely useful!.

Solved Part C Using Known Logical Equivalences Standard Chegg We demonstrated that a → (b → c) is logically equivalent to (a∧b) → c using logical equivalences and properties of implication. by rewriting the implications and using de morgan's laws, we simplified the expressions and established the equivalence. What are logical equivalences and why are they useful? definition: compound propositions p and q are logically equivalent exactly when p q is a tautology. the notation p q means that p and q are logically equivalent. logical equivalences are extremely useful!. 1.4.2 truth tables to prove logical equivalence. equi (c) ¬p → q and p ∨ q the columns for ¬p → q and p ∨ q are the same. Use part (a) to explain why that can be done by establishing the validity of the argument. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. upvoting indicates when questions and answers are useful. what's reputation and how do i get it? instead, you can save this post to reference later. how to prove this logical equivalence using different laws?. Two expressions are logically equivalent by developing a series of logically equivalent statements. to prove that a is logically equivalent to b, produce a series of equivalences beginning with a and ending with b.

Solved Part C Using Known Logical Equivalences Standard Chegg 1.4.2 truth tables to prove logical equivalence. equi (c) ¬p → q and p ∨ q the columns for ¬p → q and p ∨ q are the same. Use part (a) to explain why that can be done by establishing the validity of the argument. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. upvoting indicates when questions and answers are useful. what's reputation and how do i get it? instead, you can save this post to reference later. how to prove this logical equivalence using different laws?. Two expressions are logically equivalent by developing a series of logically equivalent statements. to prove that a is logically equivalent to b, produce a series of equivalences beginning with a and ending with b.