Tensor Tutorial Part 1 Of 6 Groups And Representations

Tensor Prod Pdf Tensor Basis Linear Algebra A tensor itself is a linear combination of let’s say generic tensors of the form . in the case of one doesn’t speak of tensors, but of vectors instead, although strictly speaking they would be called monads. Tensor : multidimensional array :: linear transformation : matrix. the short of it is, tensors and multidimensional arrays are different types of object; the first is a type of function, the second is a data structure suitable for representing a tensor in a coordinate system.

Tensor Analysis Chapter 1 Pdf Euclidean Vector Tensor Every tensor is associated with a linear map that produces a scalar. for instance, a vector can be identified with a map that takes in another vector (in the presence of an inner product) and produces a scalar. What is the difference between a matrix and a tensor? or, what makes a tensor, a tensor? i know that a matrix is a table of values, right? but, a tensor?. Tensor in new latin tensor means "that which stretches". the mathematical object is so named because an early application of tensors was the study of materials stretching under tension. Tl;dr summary from what i know all quantities are tensors , divided into rank 0,rank 1 ,rank 2 , rank 3 rank ( n )according to their components which is 3^n . current is supposed to be a scalar quantity right? it does not follow vector rules . our book says it is a tensor quantity (ofcourse yes) but my question is "is current truly a scalar quantity" ? if a bunch of electron were to drift.

General Tensor Pdf Tensor Linear Algebra Tensor in new latin tensor means "that which stretches". the mathematical object is so named because an early application of tensors was the study of materials stretching under tension. Tl;dr summary from what i know all quantities are tensors , divided into rank 0,rank 1 ,rank 2 , rank 3 rank ( n )according to their components which is 3^n . current is supposed to be a scalar quantity right? it does not follow vector rules . our book says it is a tensor quantity (ofcourse yes) but my question is "is current truly a scalar quantity" ? if a bunch of electron were to drift. This is a beginner's question on what exactly is a tensor product, in laymen's term, for a beginner who has just learned basic group theory and basic ring theory. i do understand from th. A rank 3 tensor inputs three generalized vectors (i.e. either a vector or their dual vector), and spits out a scalar. one can also think of it as inputting 2 generalized vectors (or a rank 2 tensor), and outputting a vector, or inputting 1 generalized vector, and outputing 2 vectors (or a rank 2 tensor). For example, in 3d, the dual tensor to a vector represents a plane (vector plane fully spans 3d space). tensor densities are a bit of a cheat when talking about integrals of tensors with respect to volumes. 16 why does tensor rotation require multiplication by the rotation matrix twice, once from the right and once from the left by the inverse? if t t is the tensor i wish to rotate and r r is the rotation matrix, why isn't t′ = rt t = r t but is t = rtr−1 t = r t r 1?.

Tutorial Sheet 1 To 6 Pdf Tensor Euclidean Vector This is a beginner's question on what exactly is a tensor product, in laymen's term, for a beginner who has just learned basic group theory and basic ring theory. i do understand from th. A rank 3 tensor inputs three generalized vectors (i.e. either a vector or their dual vector), and spits out a scalar. one can also think of it as inputting 2 generalized vectors (or a rank 2 tensor), and outputting a vector, or inputting 1 generalized vector, and outputing 2 vectors (or a rank 2 tensor). For example, in 3d, the dual tensor to a vector represents a plane (vector plane fully spans 3d space). tensor densities are a bit of a cheat when talking about integrals of tensors with respect to volumes. 16 why does tensor rotation require multiplication by the rotation matrix twice, once from the right and once from the left by the inverse? if t t is the tensor i wish to rotate and r r is the rotation matrix, why isn't t′ = rt t = r t but is t = rtr−1 t = r t r 1?.

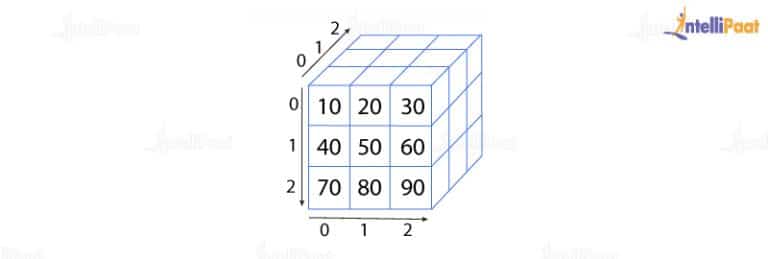
Tensorflow Tutorial For Beginners Updated 2025 For example, in 3d, the dual tensor to a vector represents a plane (vector plane fully spans 3d space). tensor densities are a bit of a cheat when talking about integrals of tensors with respect to volumes. 16 why does tensor rotation require multiplication by the rotation matrix twice, once from the right and once from the left by the inverse? if t t is the tensor i wish to rotate and r r is the rotation matrix, why isn't t′ = rt t = r t but is t = rtr−1 t = r t r 1?.

Immerse Yourself in Art, Culture, and Creativity: Celebrate the beauty of artistic expression with our Tensor Tutorial Part 1 Of 6 Groups And Representations resources. From art forms to cultural insights, we'll ignite your imagination and deepen your appreciation for the diverse tapestry of human creativity.

Tensor Tutorial part 1 of 6 - Groups and Representations

Tensor Tutorial part 1 of 6 - Groups and Representations

Tensor Tutorial part 1 of 6 - Groups and Representations Anna Seigal: "Tensors in Statistics and Data Analysis" Tensor Tutorial part 2 of 6 - Rotation Groups Tensor Tutorial part 3 of 6 - SO(3) Metric Tensor Part 1.wmv Quiz 1 Doubt Clearing Session | T2-2025 Tensor Tutorial part 6 of 6 - Tensors and How They Transform Visualization of tensors - part 1 Introduction to Tensors Tensors for Beginners 1: Forward and Backward Transformations (REMAKE) Groups & Representations - Tensors #2 PyTorch or Tensorflow? Which Should YOU Learn! Group Theory L25V2: Tensor Products of Vector Representations RotationOperatorPt1.wmv Joseph Landsberg: "Introduction to the Geometry of Tensors (Part 1/2)" Group Theory L25V2: Tensor Products of Vector Representations

Conclusion

Following an extensive investigation, it is unmistakable that the content delivers educational facts with respect to Tensor Tutorial Part 1 Of 6 Groups And Representations. From start to finish, the journalist portrays significant acumen related to the field. Notably, the chapter on notable features stands out as a crucial point. The text comprehensively covers how these components connect to build a solid foundation of Tensor Tutorial Part 1 Of 6 Groups And Representations.

Besides, the essay does a great job in clarifying complex concepts in an clear manner. This straightforwardness makes the analysis valuable for both beginners and experts alike. The author further elevates the review by weaving in applicable cases and real-world applications that put into perspective the conceptual frameworks.

A supplementary feature that distinguishes this content is the detailed examination of several approaches related to Tensor Tutorial Part 1 Of 6 Groups And Representations. By analyzing these alternate approaches, the publication provides a balanced picture of the issue. The comprehensiveness with which the writer handles the matter is extremely laudable and sets a high standard for analogous content in this area.

In summary, this piece not only instructs the reader about Tensor Tutorial Part 1 Of 6 Groups And Representations, but also prompts additional research into this engaging area. For those who are just starting out or an experienced practitioner, you will discover useful content in this exhaustive post. Many thanks for your attention to the piece. If you need further information, please do not hesitate to reach out using the discussion forum. I am excited about your thoughts. For more information, you will find a number of connected write-ups that you will find helpful and complementary to this discussion. Happy reading!