1 5 Analyzing Graphs Of Functions

1 5 Analyzing Graphs Of Functions 1.5 analyzing graphs of functions what you should learn use the vertical line test for functions. find the zeros of functions. determine intervals on which functions are increasing or decreasing and determine relative maximum and relative minimum values of functions. A set of points in a coordinate plane is the graph of y as a function of x if and only if no vertical line intersects the graph at more than one point. study with quizlet and memorize flashcards containing terms like vertical line test, zeros of a function, increasing function and more.

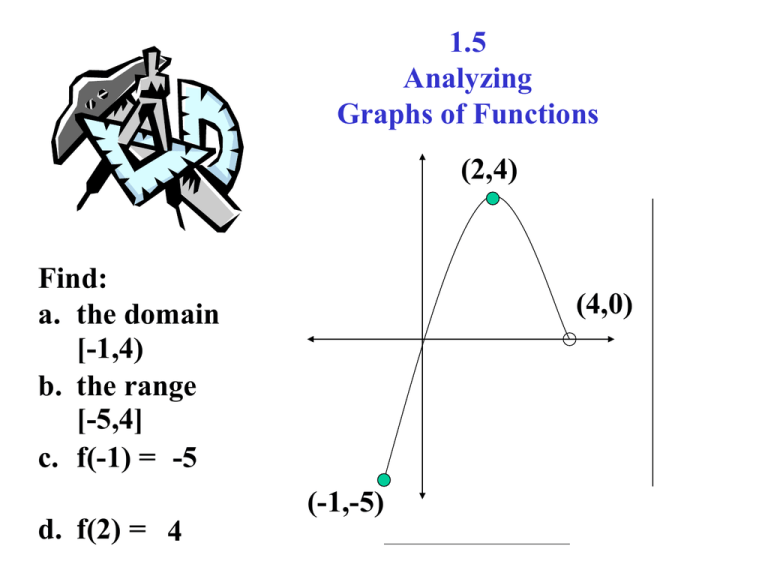
1 5 Analyzing Graphs Of Functions Learn how to analyze graphs of functions in precalculus, including polynomial functions, rational functions, radical functions, odd functions, and even functions. Once pre calculus students are confident in their knowledge of functions and relations, they move on to analyzing graphs of functions and relations (including identifying x and y intercepts, zeros, symmetry, even and odd functions). Sheet 1.5 – analyzing graphs of functions fi. d . he domain and the range of the function. 1. use the graph of the fun. ti. n to find. ues. 2. a) f ( 2) b) f ( 1) c) d) f (1) use the vertical line tes. t. termine whether y is a function of x. 4. f. Summary of general properties, asymptotes, limits, and differentiability of a function. given a set of information on the key properties of a function, you can sketch the graph. before we proceed, make an attempt to summarize for what you think are key properties.

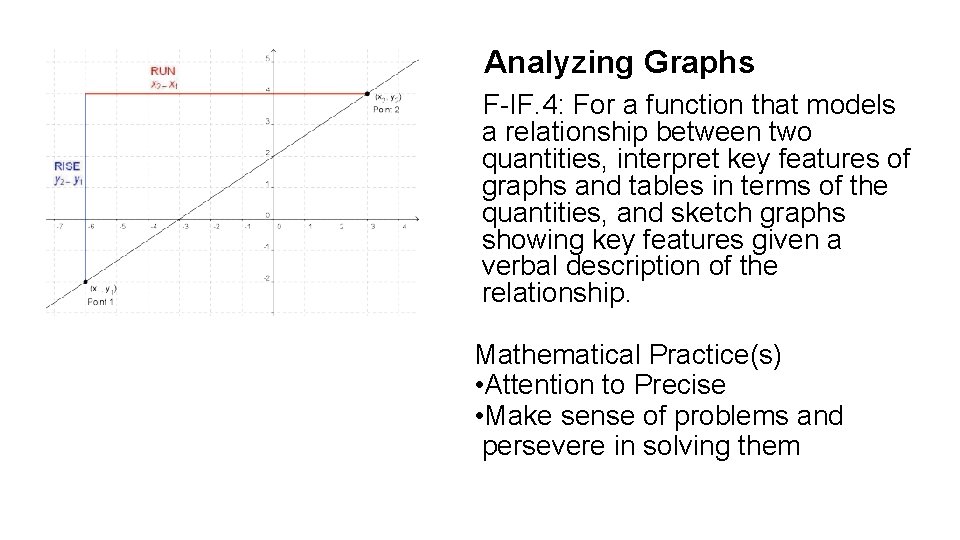
Unit 1 Analyzing Functions Analyzing Graphs Fif 4 Sheet 1.5 – analyzing graphs of functions fi. d . he domain and the range of the function. 1. use the graph of the fun. ti. n to find. ues. 2. a) f ( 2) b) f ( 1) c) d) f (1) use the vertical line tes. t. termine whether y is a function of x. 4. f. Summary of general properties, asymptotes, limits, and differentiability of a function. given a set of information on the key properties of a function, you can sketch the graph. before we proceed, make an attempt to summarize for what you think are key properties. 1.5 analyzing graphs of functions examples: find the domain and range of several graphs. vertical line test for functions: a set of points in a coordinate plane is the graph of y as a f. nction of x if and only if no vertical line int. rsects the graph at more than one point. examples: test some graphs for function or not. In this section, we’ll look briefly at four types of functions: polynomial functions, rational functions, exponential functions and logarithmic functions. what do you know about the graph of the function. 3 f ( x ) = x 9 x ? solution: we know that it is a polynomial function with odd degree and a positive leading coefficient. Which of the following graphs represent y as a function of x? find the domain and range of each function. a set of points in the xy plane is the graph of y as a function of x if and only if no vertical line intersects the graph at more than one point. a function can have at most one y intercept. def. the zeros of a function values for which. Use the vertical line test for functions. find the zeros of functions. determine intervals on which functions are increasing or decreasing and determine relative maximum and relative minimum values of functions. determine the average rate of change of a function. identify even and odd functions.

Whether you're here to learn, to share, or simply to indulge in your love for 1 5 Analyzing Graphs Of Functions, you've found a community that welcomes you with open arms. So go ahead, dive in, and let the exploration begin.

1-5 Analyzing Graphs of Functions

1-5 Analyzing Graphs of Functions

1-5 Analyzing Graphs of Functions 1 5 Analyzing Graphs of Functions 1 5 Analyzing Graphs of Functions Part 1 1 5 Analyzing Graphs of Functions Pre-Calculus 1-5 Analyzing Graphs of Functions Notes 1 5 Analyzing Graphs of Functions Lesson 1-5 Analyzing Graphs of Functions (Part 1) Section 1 5 Analyzing Graphs of FunctionA Calculus of Motion: Understand POSITION, VELOCITY, and ACCELERATION Functions Section 1 5 Analyzing Graphs of Function E mp4 Notes 1 5 Analyzing Graphs of Functions Precalculus 1.5 Analyzing Graphs of Functions Section 1 5 Analyzing Graphs of FunctionD Section 1 5 Analyzing Graphs of FunctionsB 1 5 Analyzing Graphs of Functions Part 2 Pre-Calculus 1.5: Analyzing Graphs of Functions part 1 PreCalculus: 1.5 Analyzing Graphs of Functions Lesson 1-5 Analyzing Graphs of Functions (Part 2) H-TPC: Section 1.5 - Analyzing Graphs of Functions

Conclusion

Following an extensive investigation, it is clear that this specific article supplies informative insights touching on 1 5 Analyzing Graphs Of Functions. Throughout the article, the journalist illustrates considerable expertise pertaining to the theme. Specifically, the section on contributing variables stands out as a highlight. The text comprehensively covers how these components connect to develop a robust perspective of 1 5 Analyzing Graphs Of Functions.

On top of that, the composition stands out in breaking down complex concepts in an easy-to-understand manner. This straightforwardness makes the content valuable for both beginners and experts alike. The writer further improves the examination by including germane instances and concrete applications that situate the abstract ideas.

Another element that distinguishes this content is the comprehensive analysis of diverse opinions related to 1 5 Analyzing Graphs Of Functions. By considering these various perspectives, the post offers a balanced view of the matter. The exhaustiveness with which the journalist treats the topic is highly praiseworthy and raises the bar for related articles in this area.

In summary, this post not only teaches the observer about 1 5 Analyzing Graphs Of Functions, but also stimulates additional research into this fascinating topic. Should you be a novice or a seasoned expert, you will find beneficial knowledge in this comprehensive article. Gratitude for engaging with the content. Should you require additional details, you are welcome to connect with me by means of the feedback area. I look forward to your comments. For further exploration, you can see various connected articles that might be beneficial and additional to this content. Hope you find them interesting!