Dijkstra S Algorithm Shortest Path Pdf Algorithms Algorithms And Learn all about dijkstra's shortest path algorithm for your cie a level computer science exam. this revision note includes how to write the algorithm in pseudocode. One of these is known as dijkstra’s algorithm. it was designed by dutch physicist edsger dijkstra in 1956, when he thought about how he might calculate the shortest route from rotterdam to groningen.

Dijkstra Algorithm Lecture Notes Pdf Mathematical Relations Dijkstra’s algorithm is a popular algorithm for solving single source shortest path problems having non negative edge weight in the graphs i.e., it is to find the shortest distance between two vertices on a graph. it was conceived by dutch computer scientist edsger w. dijkstra in 1956. Dijkstra’s shortest path algorithm is an algorithm used to find the shortest path between two nodes of a weighted graph. before investigating this algorithm make sure you are familiar with the terminology used when describing graphs in computer science. Dijkstra's algorithm ( ˈdaɪkstrəz dyke strəz) is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, a road network. The shortest path algorithm calculates the shortest path from a start node to each node of a connected graph. developed in 1956 by edsger w. dijsktra, it is the basis for all the apps that show you a shortest route from one place to another.

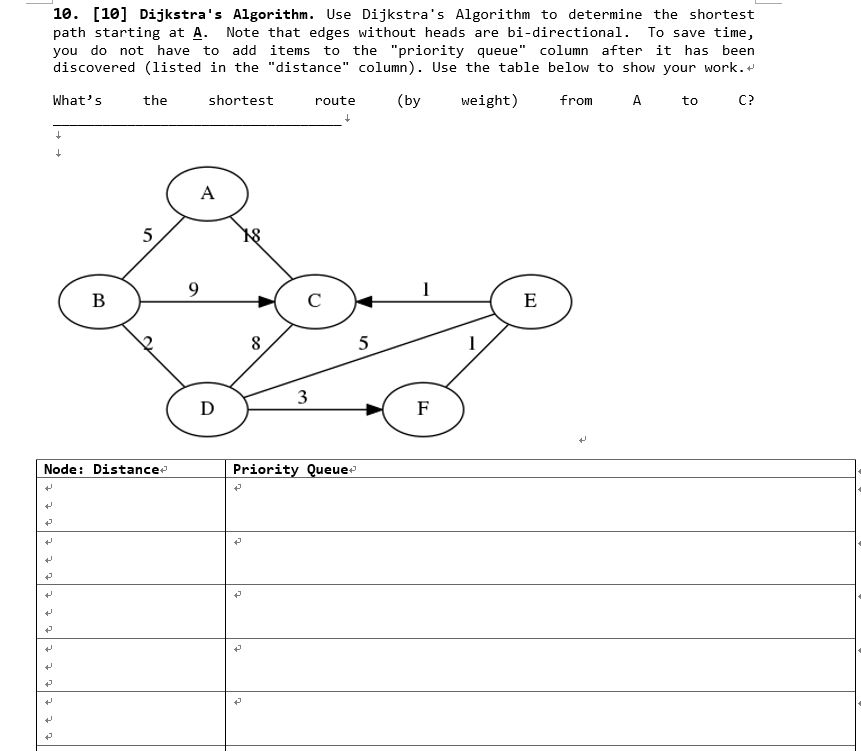
Solved Dijkstra S Algorithm Use Dijkstra S Algorithm To Chegg Dijkstra's algorithm ( ˈdaɪkstrəz dyke strəz) is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, a road network. The shortest path algorithm calculates the shortest path from a start node to each node of a connected graph. developed in 1956 by edsger w. dijsktra, it is the basis for all the apps that show you a shortest route from one place to another. Given a weighted directed graph, g g, and some starting node s s, dijkstra’s algorithm will find the shortest paths from s s to all other nodes in the graph. one constraint on using dijkstra’s algorithm is that all edge weights must be non negative. dijkstra’s algorithm is great as long as we have no negative weight edges in our graph. Goal: from one starting vertex, what are the shortest paths to each of the other vertices (for a weighted graph)? known? “computer science is no more about computers than astronomy is about telescopes.” dijkstra’s algorithm is one example of note: for some problems, greedy algorithms cannot find best answer!. Outline of this lecture recalling the bfs solution of the shortest path problem for unweighted (di)graphs. the shortest path problem for weighted digraphs. dijkstra’s algorithm. given for digraphs but easily modified to work on undirected graphs.