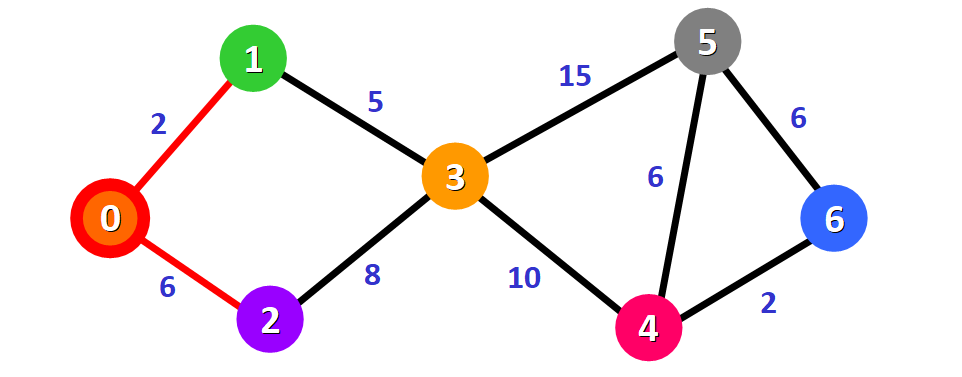
Dijkstras Shortest Path Algorithm A Detailed And Visual Introduction Dijkstra's algorithm finds the shortest path between a given node (which is called the "source node") and all other nodes in a graph. this algorithm uses the weights of the edges to find the path that minimizes the total distance (weight) between the source node and all other nodes. Dijkstra’s algorithm is a popular algorithm for solving single source shortest path problems having non negative edge weight in the graphs i.e., it is to find the shortest distance between two vertices on a graph.

Dijkstra S Shortest Path Algorithm A Detailed And Visual Introduction Dijkstra's algorithm ( ˈdaɪkstrəz dyke strəz) is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, a road network. Dijkstra's algorithm is a classic algorithm for computing the shortest path from a single source in a weighted graph. this page describes the algorithm's principles and implementation steps, and provides interactive tools that allow you to set the graph's vertices and edges, weights, and visually observe the algorithm's execution process. This image explains the basics of dijkstra's algorithm, including its purpose and the type of graphs it works with. it highlights that dijkstra finds the shortest path from a start node to all other nodes, efficiently using non negative edge weights. This algorithm finds a shortest path tree from a single source node by building a set of nodes that have a minimum distance from the source node. this algorithm uses a greedy approach in that we find the next best solution in hope that it will lead to a generalized optimal solution.

Dijkstra S Shortest Path Algorithm A Detailed And Visual Introduction This image explains the basics of dijkstra's algorithm, including its purpose and the type of graphs it works with. it highlights that dijkstra finds the shortest path from a start node to all other nodes, efficiently using non negative edge weights. This algorithm finds a shortest path tree from a single source node by building a set of nodes that have a minimum distance from the source node. this algorithm uses a greedy approach in that we find the next best solution in hope that it will lead to a generalized optimal solution. Dijkstra's algorithm can be used to calculate the shortest paths from a start node to each node of the graph. the algorithm can be applied to both directed and undirected graphs. however, it is important that the edge weights must not be negative. a classical application area for dijkstra's algorithm is route planning. Efficiently find next vertex in the order using a data structure. what about all pairs shortest paths? can do better than |v | · o(|v | · |e|) for general graphs with negative weights (next time!). Dijkstra's algorithm a greedy algorithm which grows the set s of \shortest path solved" vertices. s has some vertices where shortest path from s is known (blue edges). s has some outgoing edges (from s to outside s) (fringe edges in purple) (fringe vertices are those accessible by a fringe edge) on, dijkstra's algorithm will add the fringe ver. Finding the shortest path between two points is a common problem in the real world, from planning routes on road maps to determining how to efficiently route data across computer networks. in the 1950s, mathematician edsger dijkstra thought deeply about this problem and designed an elegant solution in the form of dijkstra‘s shortest path algorithm.