
Examples Of A Functions As An Ordered Pairs Pdf Function A function. note the example below the y values are used to create the ordered pairs, and the resulting graph has two values for a given x value so the relation x = y2 is not a function. Relation – any set of ordered pairs. function – a correspondence from a first set, called the domain, to a second set, called the range, such that each element in the domain corresponds to exactly one element in the range. example 1: graph the following relation representing y.
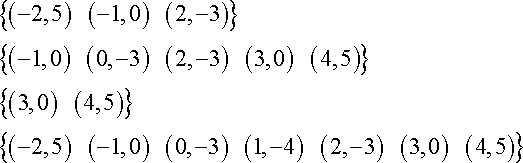
Ordered Pairs Function Examples A function can be visualized as an input output device and represented using ordered pairs, diagrams, graphs or equations. to evaluate a function means replacing inputs (x values) with given values and calculating the corresponding outputs. {all second elements of ordered pairs} { 40,0,100} {40,32,212} function: a function f of x is a correspondence that associates each x in the domain exactly one y in the range. if x is the input value and y is the output value, we call y the value of x under f. (unique pairing – domain elements do not repeat). 3.1 functions a relation is a set of ordered pairs (x, y). example: the set {(1,a), (1, b), (2,b), (3,c), (3, a), (4,a)} is a relation ith the same first component. sometimes we say that a function is a rule (correspondence) that assigns to each element of one set , x, one and only. When a relation is given as ordered pairs, the x coordinates are inputs and the y coordinates are outputs. a relation that pairs each input with exactly one output is a function. describing a function. work with a partner. functions can be described in many ways.
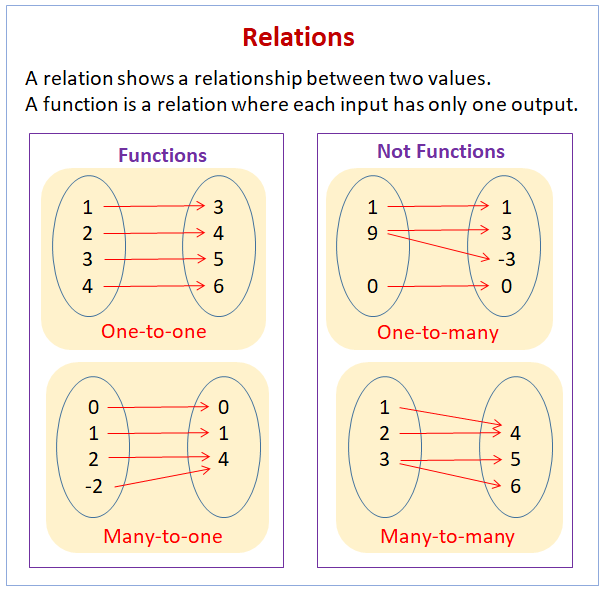
Ordered Pairs Function Examples 3.1 functions a relation is a set of ordered pairs (x, y). example: the set {(1,a), (1, b), (2,b), (3,c), (3, a), (4,a)} is a relation ith the same first component. sometimes we say that a function is a rule (correspondence) that assigns to each element of one set , x, one and only. When a relation is given as ordered pairs, the x coordinates are inputs and the y coordinates are outputs. a relation that pairs each input with exactly one output is a function. describing a function. work with a partner. functions can be described in many ways. It is possible to construe functions as sets, in particular, as sets of ordered pairs: with f:a b , we may consider the set of all pairs (a, f(a)) with a ̨ a ; this set is called the graph of the function f : graph(f) = {(a, f(a)) : a ̨ a} . def representation of functions that we use in for in exp:. 2:1 practice: relations and functions – a comprehensive guide understanding relations and functions is fundamental to grasping higher level mathematical concepts. this comprehensive guide will delve into the intricacies of these core mathematical objects, providing clear explanations and practical examples to solidify your understanding. we will focus on the crucial distinctions between. An ordered pair Ð ß ,Ñ is is built from two objects ß and ,Þ as the name suggests, the “order” matters: Ð ß ,Ñ and Ð,ß Ñ are two different ordered pairs (unless œ ,Ñ . for two ordered pairs, Ð ß ,Ñ œ Ð ß .Ñ iff œ and , œ .Þ. Relation: a relation is a set of ordered pairs. the set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range. function: a function is a relation in which each possible input value leads to exactly one output value.
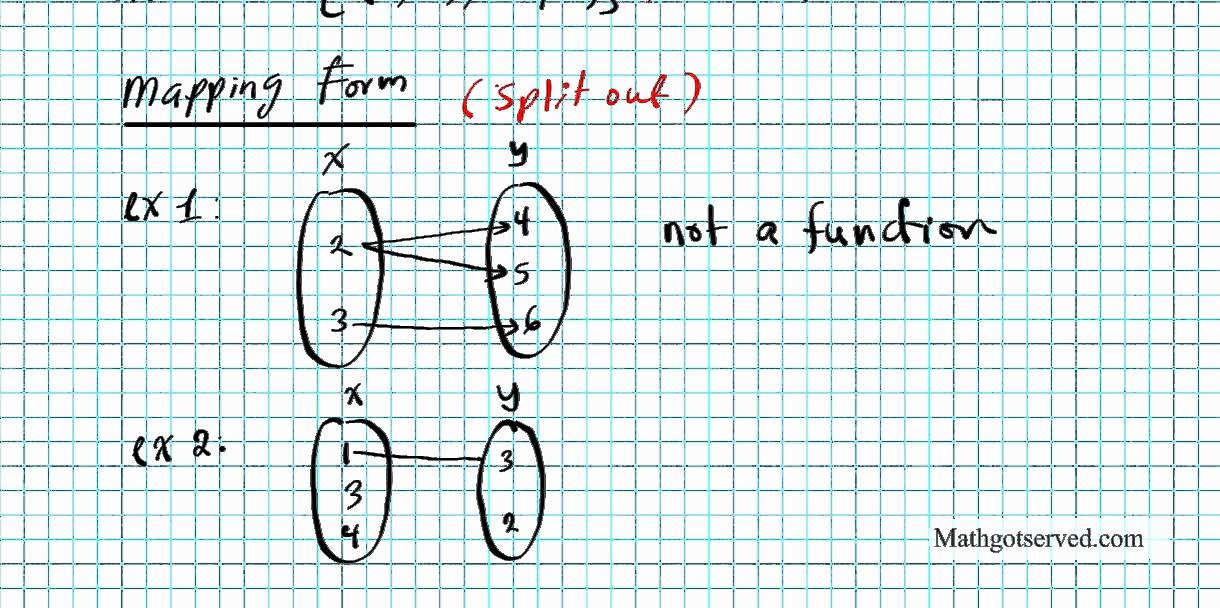
Ordered Pairs Function Examples It is possible to construe functions as sets, in particular, as sets of ordered pairs: with f:a b , we may consider the set of all pairs (a, f(a)) with a ̨ a ; this set is called the graph of the function f : graph(f) = {(a, f(a)) : a ̨ a} . def representation of functions that we use in for in exp:. 2:1 practice: relations and functions – a comprehensive guide understanding relations and functions is fundamental to grasping higher level mathematical concepts. this comprehensive guide will delve into the intricacies of these core mathematical objects, providing clear explanations and practical examples to solidify your understanding. we will focus on the crucial distinctions between. An ordered pair Ð ß ,Ñ is is built from two objects ß and ,Þ as the name suggests, the “order” matters: Ð ß ,Ñ and Ð,ß Ñ are two different ordered pairs (unless œ ,Ñ . for two ordered pairs, Ð ß ,Ñ œ Ð ß .Ñ iff œ and , œ .Þ. Relation: a relation is a set of ordered pairs. the set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range. function: a function is a relation in which each possible input value leads to exactly one output value.

Function Ordered Pairs Examples An ordered pair Ð ß ,Ñ is is built from two objects ß and ,Þ as the name suggests, the “order” matters: Ð ß ,Ñ and Ð,ß Ñ are two different ordered pairs (unless œ ,Ñ . for two ordered pairs, Ð ß ,Ñ œ Ð ß .Ñ iff œ and , œ .Þ. Relation: a relation is a set of ordered pairs. the set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range. function: a function is a relation in which each possible input value leads to exactly one output value.