Myopenmath This video approaches finding a maximum volume of an open top box as a polynomial function. we will use desmos to find the highest value. we will also use desmos to visualize. Find the value of x x x that maximizes the volume of the open top box. first, we’ll sketch an image of the flat piece of paper. the diagram shows the 5 × 7 5\times7 5 × 7 dimensions of the paper, and the x × x x\times x x × x square that was cut out of each corner.

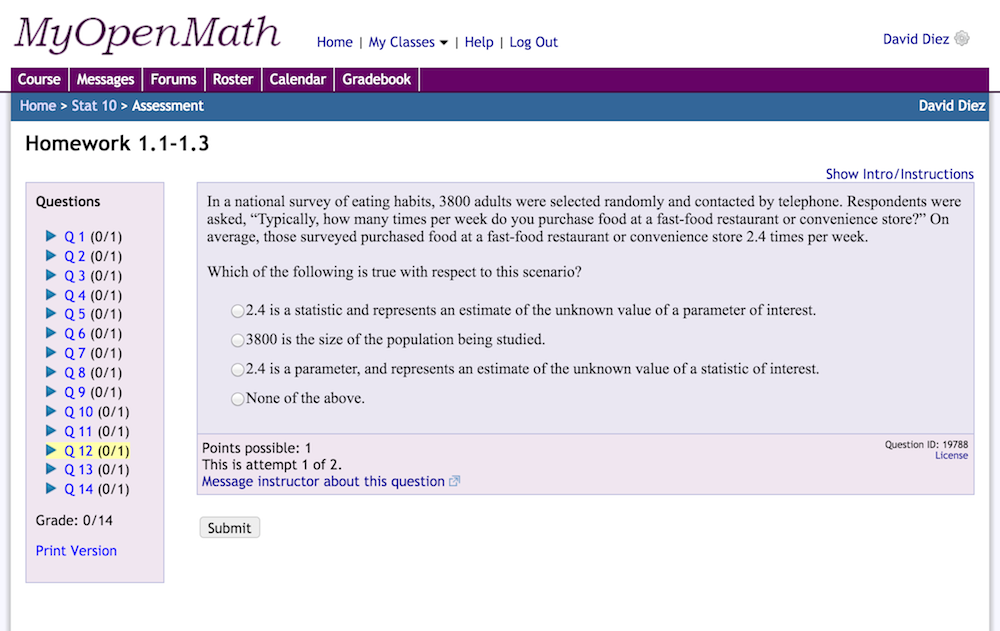
Myopenmath Explore math with our beautiful, free online graphing calculator. graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Calculate the volume at the critical points (peaks) and determine which one gives the maximum volume. the maximum volume for the box is approximately 96.8 cubic inches. Algebra 2 project: optimizing an open top box in this project you will design and construct an open top box that holds the maximum volume for a given size of material. read p. 447 (pdf p 465) # 101 in the algebra 2 book: study the drawing to see how the box is designed, and what the variable x represents. answer part (a) and part (b) of the. 5: 55 5 g 90 myopenmath open box problem. an open box (top open) is made from a rectangular material of dimensions a=10 inches by b=10 inches by cutting a square of side x at each corner and turning up the sides (see the figure). determine the value of x that results in a box with the maximum volume.following the steps to solve the problem.

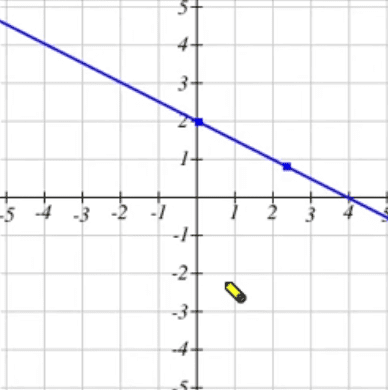
Myopenmath Answers Easy Way To Top Grades Algebra 2 project: optimizing an open top box in this project you will design and construct an open top box that holds the maximum volume for a given size of material. read p. 447 (pdf p 465) # 101 in the algebra 2 book: study the drawing to see how the box is designed, and what the variable x represents. answer part (a) and part (b) of the. 5: 55 5 g 90 myopenmath open box problem. an open box (top open) is made from a rectangular material of dimensions a=10 inches by b=10 inches by cutting a square of side x at each corner and turning up the sides (see the figure). determine the value of x that results in a box with the maximum volume.following the steps to solve the problem. This video explains how to analyze the graph of a volume function of an open top box to determine the maximum volume. the box is formed but cutting corners out of the corners of a. Cut four corners out of a sheet of cardboard to form a box with the maximum volume possible: 1 a = 2 2. Determine the value 61119 min of x that results in a box the maximum volume. # (1) express the volume v as a function of x: v = 195x 56x^2 4x^3. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: open box problem. How to maximize the volume of a box using the first derivative of the volume. a volume optimization problem with solution. a sheet of metal 12 inches by 10 inches is to be used to make an open box. squares of equal sides x x are cut out of each corner then the sides are folded to make the box. find the value of x x that makes the volume maximum.

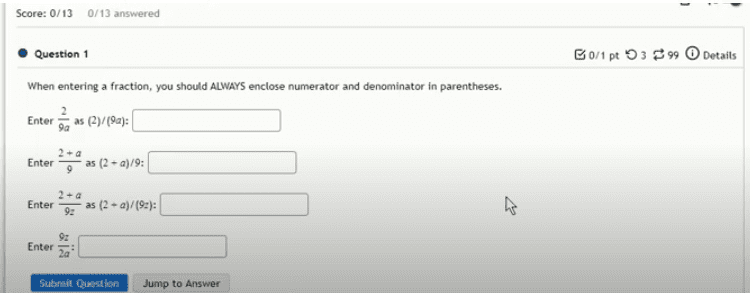
Myopenmath Answers Easy Way To Top Grades This video explains how to analyze the graph of a volume function of an open top box to determine the maximum volume. the box is formed but cutting corners out of the corners of a. Cut four corners out of a sheet of cardboard to form a box with the maximum volume possible: 1 a = 2 2. Determine the value 61119 min of x that results in a box the maximum volume. # (1) express the volume v as a function of x: v = 195x 56x^2 4x^3. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: open box problem. How to maximize the volume of a box using the first derivative of the volume. a volume optimization problem with solution. a sheet of metal 12 inches by 10 inches is to be used to make an open box. squares of equal sides x x are cut out of each corner then the sides are folded to make the box. find the value of x x that makes the volume maximum.

Myopenmath Answers Easy Way To Top Grades Determine the value 61119 min of x that results in a box the maximum volume. # (1) express the volume v as a function of x: v = 195x 56x^2 4x^3. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: open box problem. How to maximize the volume of a box using the first derivative of the volume. a volume optimization problem with solution. a sheet of metal 12 inches by 10 inches is to be used to make an open box. squares of equal sides x x are cut out of each corner then the sides are folded to make the box. find the value of x x that makes the volume maximum.

Myopenmath Answers Easy Way To Top Grades