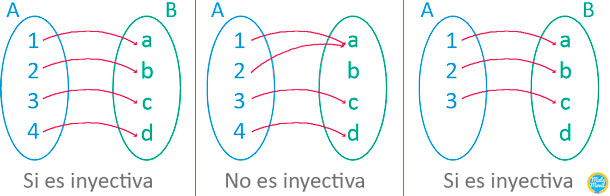
Funciones Inyectivas Suyectiva Y Biyectivas Segunda Parte Funciones inyectivas, sobreyectivas y biyectivas: contenidos teóricos, ejercicios resueltos, imágenes, animaciones y formularios de física y matemáticas. Funciones inyectivas, suyectiva y biyectivas segunda parte la función es inyectiva si cada elemento de la imagen tiene un único elemento del dominio asociado. una función es inyectiva si para valores distintos del dominio x0 ≠ x1 se cumple que f (x0) ≠ f (x1).

Ejercicios Resueltos De Funciones Inyectivas Sobreyectivas Y Biyectivas Pdf En este artículo explicamos la clasificación de funciones según la relación entre sus elementos en inyectivas, sobreyectivas y biyectivas. analizamos las definiciones, ejemplos, cómo se comportan las gráficas y cómo reconocer a que grupo pertenece una función. Las funciones inyectivas, sobreyectivas y biyectivas son las herramientas básicas para comparar el número de elementos de dos conjuntos. observando el digrafo de una función biyectiva f : a !. La inyectividad, sobreyectividad y biyectividad dan información acerca de cómo se relacionan los elementos del conjunto inicial x con el conjunto final y. cabe recordar que una función f es una relación que asigna a los elementos de un primer conjunto (conjunto inicial x) un elemento de un segundo conjunto (conjunto final y). La función inyectiva es la siguiente: f: x > y es inyectiva solamente si para los elementos del conjunto x a y b se cumple que f (a) es igual a f (b) cuando a es igual a b.

Pdf Funciones Inyectivas Suryectivas Y Biyectivas La inyectividad, sobreyectividad y biyectividad dan información acerca de cómo se relacionan los elementos del conjunto inicial x con el conjunto final y. cabe recordar que una función f es una relación que asigna a los elementos de un primer conjunto (conjunto inicial x) un elemento de un segundo conjunto (conjunto final y). La función inyectiva es la siguiente: f: x > y es inyectiva solamente si para los elementos del conjunto x a y b se cumple que f (a) es igual a f (b) cuando a es igual a b. Siguiendo con este tema, ahora vamos a estudiar tres tipos de funciones: las inyectivas, suprayectivas y finalmente las inyectivas. hemos hablado anteriormente de las primeras dos, ahora estudiaremos algunas equivalencias de las definiciones vistas en un principio y algunos resultados interesantes. Este documento explora en detalle los conceptos de funciones inyectivas (uno a uno), sobreyectivas (suprayectivas u "onto") y biyectivas, proporcionando definiciones formales, ejemplos concretos y representaciones gráficas. Las funciones inyectivas, sobreyectivas y biyectivas son conceptos fundamentales en matemáticas. si aprendes a dominar estos conceptos, podrás entender mejor el comportamiento de las funciones y resolver problemas matemáticos con mayor facilidad. En este artículo, exploraremos las definiciones de cada uno de estos tipos de funciones, cómo se diferencian entre sí y algunos ejemplos prácticos que te ayudarán a visualizarlos.

Funciones Inyectivas Suprayectivas Y Biyectivas Pdf Siguiendo con este tema, ahora vamos a estudiar tres tipos de funciones: las inyectivas, suprayectivas y finalmente las inyectivas. hemos hablado anteriormente de las primeras dos, ahora estudiaremos algunas equivalencias de las definiciones vistas en un principio y algunos resultados interesantes. Este documento explora en detalle los conceptos de funciones inyectivas (uno a uno), sobreyectivas (suprayectivas u "onto") y biyectivas, proporcionando definiciones formales, ejemplos concretos y representaciones gráficas. Las funciones inyectivas, sobreyectivas y biyectivas son conceptos fundamentales en matemáticas. si aprendes a dominar estos conceptos, podrás entender mejor el comportamiento de las funciones y resolver problemas matemáticos con mayor facilidad. En este artículo, exploraremos las definiciones de cada uno de estos tipos de funciones, cómo se diferencian entre sí y algunos ejemplos prácticos que te ayudarán a visualizarlos.

Funciones Inyectivas Sobreyectivas Y Biyectivas Quiz Las funciones inyectivas, sobreyectivas y biyectivas son conceptos fundamentales en matemáticas. si aprendes a dominar estos conceptos, podrás entender mejor el comportamiento de las funciones y resolver problemas matemáticos con mayor facilidad. En este artículo, exploraremos las definiciones de cada uno de estos tipos de funciones, cómo se diferencian entre sí y algunos ejemplos prácticos que te ayudarán a visualizarlos.