Functions In C

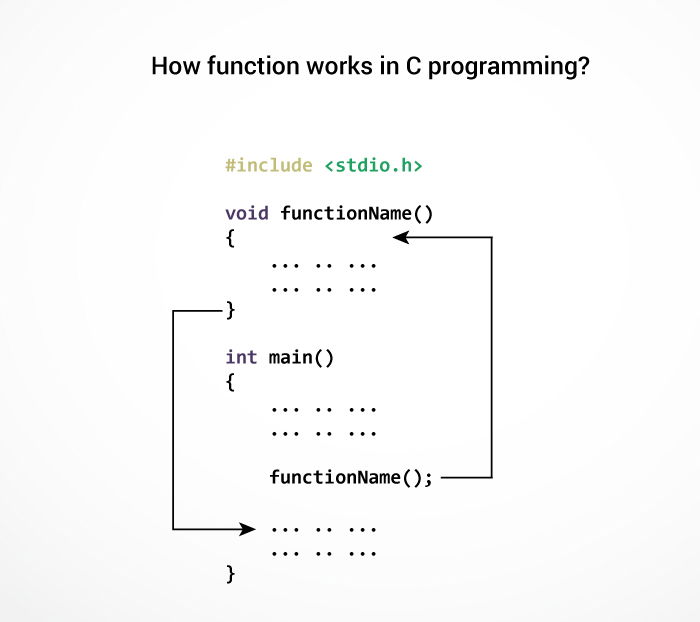
C Functions What is a function? a function relates an input to an output. it is like a machine that has an input and an output. and the output is related somehow to the input. " f (x) = " is the classic way of writing a function. and there are other ways, as you will see!. In mathematics, a function from a set x to a set y assigns to each element of x exactly one element of y. [1] the set x is called the domain of the function [2] and the set y is called the codomain of the function. [3] functions were originally the idealization of how a varying quantity depends on another quantity.

C Functions Defining And Calling Functions Codelucky Function, in mathematics, an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable). functions are ubiquitous in mathematics and are essential for formulating physical relationships in the sciences. Functions define the relationship between two variables, one is dependent and the other is independent. function in math is a relation f from a set a (the domain of the function) to another set b (the co domain of the function). explore with concept, definition, types, and examples. Functions are one of the most fundamental concepts in mathematics, serving as a cornerstone for topics in algebra, calculus and beyond. basics of functions are stepping stone to success in functions which include the definition of a functions, its notation, domain and range and the inverse functions. This topic covers: evaluating functions domain & range of functions graphical features of functions average rate of change of functions function combination and composition function transformations (shift, reflect, stretch) piecewise functions inverse functions two variable functions.

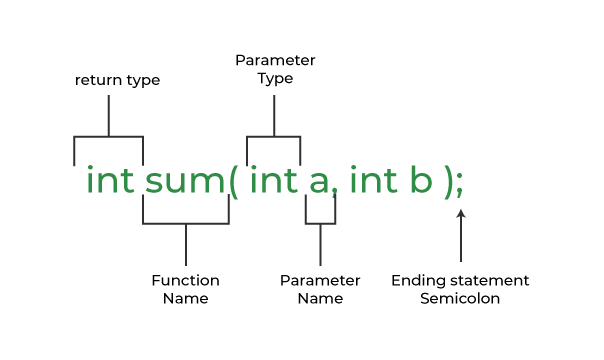
C Functions Geeksforgeeks Functions are one of the most fundamental concepts in mathematics, serving as a cornerstone for topics in algebra, calculus and beyond. basics of functions are stepping stone to success in functions which include the definition of a functions, its notation, domain and range and the inverse functions. This topic covers: evaluating functions domain & range of functions graphical features of functions average rate of change of functions function combination and composition function transformations (shift, reflect, stretch) piecewise functions inverse functions two variable functions. Our development of the function concept is a modern one, but quite quick, particularly in light of the fact that today’s definition took over 300 years to reach its present state. we begin with the definition of a relation. we use the notation (2, 4) to denote what is called an ordered pair. In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. A function is a special relation or method connecting each member of set a to a unique member of set b via a defined relation. set a is called the domain and set b is called the co domain of the function. a function in mathematics from set a to set b is defined as, f = { (a,b)| ∀ a ∈ a, b ∈ b}. What is a function in maths? a function in maths is a special relationship among the inputs (i.e. the domain) and their outputs (known as the codomain) where each input has exactly one output, and the output can be traced back to its input. an example of a simple function is f (x) = x 2.

Welcome to our blog, where Functions In C takes the spotlight and fuels our collective curiosity. From the latest trends to timeless principles, we dive deep into the realm of Functions In C, providing you with a comprehensive understanding of its significance and applications. Join us as we explore the nuances, unravel complexities, and celebrate the awe-inspiring wonders that Functions In C has to offer.

Conclusion

Upon a thorough analysis, one can see that this particular article gives helpful data related to Functions In C. All the way through, the content creator portrays a deep understanding in the field. Importantly, the analysis of fundamental principles stands out as a major point. The author meticulously explains how these elements interact to create a comprehensive understanding of Functions In C.

In addition, the piece shines in deciphering complex concepts in an accessible manner. This accessibility makes the content beneficial regardless of prior expertise. The expert further elevates the discussion by including appropriate instances and tangible use cases that provide context for the intellectual principles.

An additional feature that sets this article apart is the detailed examination of different viewpoints related to Functions In C. By analyzing these diverse angles, the post offers a balanced view of the theme. The meticulousness with which the content producer tackles the matter is extremely laudable and offers a template for comparable publications in this discipline.

In conclusion, this write-up not only instructs the observer about Functions In C, but also encourages further exploration into this captivating theme. If you are just starting out or a veteran, you will find worthwhile information in this thorough write-up. Thank you sincerely for this comprehensive write-up. If you have any inquiries, do not hesitate to drop a message with our messaging system. I am eager to your thoughts. For more information, here is a few associated write-ups that you will find beneficial and complementary to this discussion. Hope you find them interesting!