Gradient Vector Applications Example 1

Gradient Vector At Getdrawings Free Download An example of f (x,y) and finding the gradient vector at a point and interpreting the gradient vector to find direction of maximum rate of change. Applications of the gradient evaluating the gradient at a point meaning of the gradient in 1 variable calculus, the derivative gives you an equation for the slope at any x value along f(x). you can then plug in an x value to find the actual slope at that point.

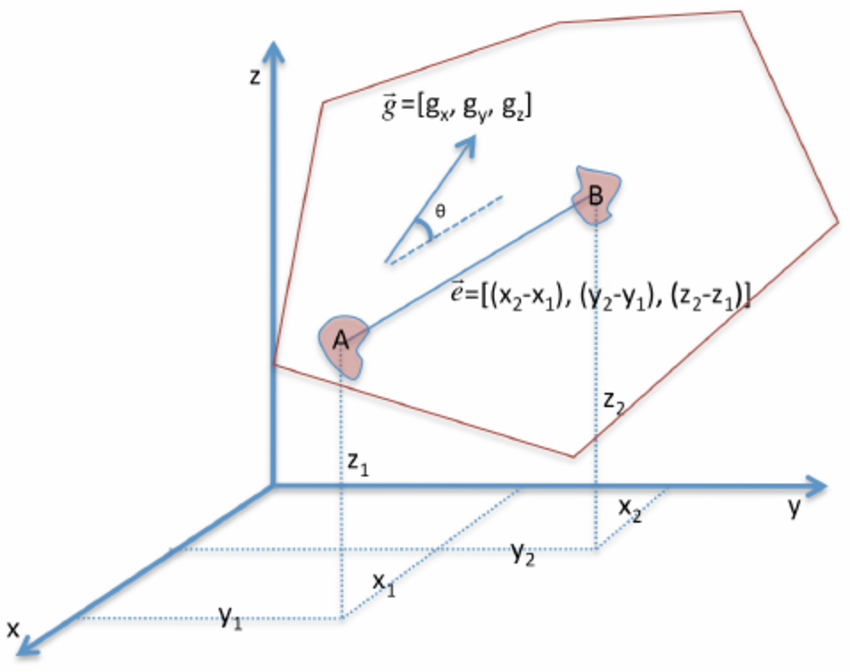
Gradient Vector At Vectorified Collection Of Gradient Vector Free Example 1 find the tangent plane and normal line to x2 y2 z2 = 30 x 2 y 2 z 2 = 30 at the point (1,−2,5) (1, 2, 5). in this section discuss how the gradient vector can be used to find tangent planes to a much more general function than in the previous section. 2 examples of gradient 1. if (x; y; z) = 3x2y y3z2, nd r (or grad ) at the point (1; 2; 1). Nt and applications today: some fun applications of . ar. ial derivatives! 1. the gradient vector now that we’ve calculated things like fx or fy, you might ask: what if w. put them together? this is the idea behi. 2xy y2, x2 2xy not. : ∇f is a vector. think of it as the “derivative” of f , tells you in which di. in(yz) ln(yz) x date: frid. 2. gradient (grad) the gradient of a function, f(x, y), in two dimensions is defined as: ∂f ∂f gradf(x, y) = ∇f(x, y) = i j . ∂x ∂y the gradient of a function is a vector field. it is obtained by applying the vector operator ∇ to the scalar function f(x, y) . such a vector field is called a gradient (or conservative) vector field.

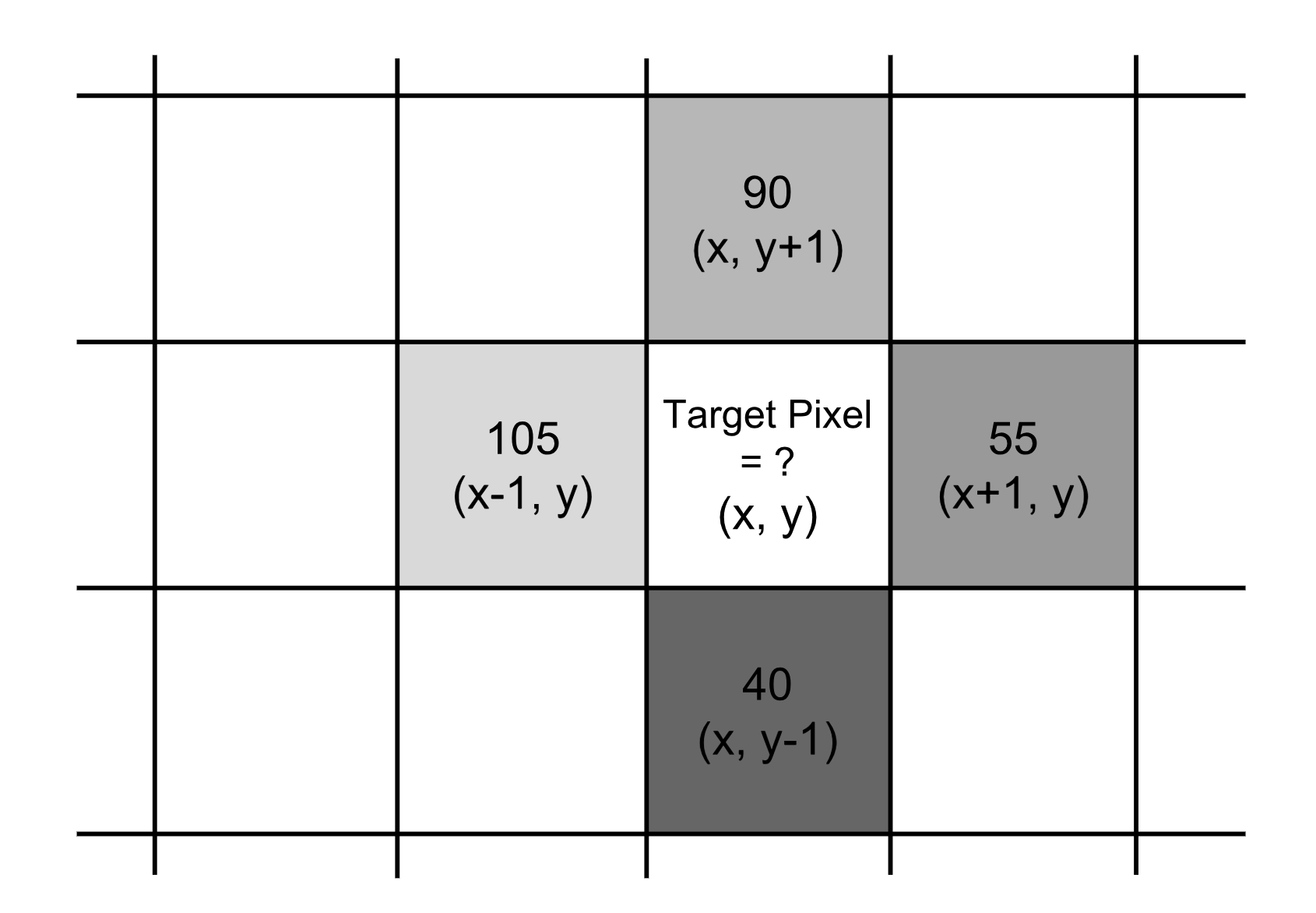
Gradient Vector At Vectorified Collection Of Gradient Vector Free Nt and applications today: some fun applications of . ar. ial derivatives! 1. the gradient vector now that we’ve calculated things like fx or fy, you might ask: what if w. put them together? this is the idea behi. 2xy y2, x2 2xy not. : ∇f is a vector. think of it as the “derivative” of f , tells you in which di. in(yz) ln(yz) x date: frid. 2. gradient (grad) the gradient of a function, f(x, y), in two dimensions is defined as: ∂f ∂f gradf(x, y) = ∇f(x, y) = i j . ∂x ∂y the gradient of a function is a vector field. it is obtained by applying the vector operator ∇ to the scalar function f(x, y) . such a vector field is called a gradient (or conservative) vector field. The gradient vector is designed to point in the direction of the greatest initial increase on your curve surface etc. Example 1 find the directional derivative of f (x, y) = 1 2x√y at (3, 4) in the direction of v = h4, −3i. solution. first we compute the partial derivatives: thus. Gradient vector applications 1. suppose fx(2; 4) = 3 and fy(2; 4) = 8. find the directional derivative of f at (2; 4) in the direction of h5; 0i. 2. find a unit vector in the direction in which f(x; y; z) = x2yz increases most rapidly at p (1; 1; 2). what is the rate of increase in this direction? 3. find two unit vectors which are normal to x2. Gradient vector applications the first and most obvious application of gradient vectors is to edge detection. you can see in the gradient images how large gradient values correspond to strong edges in the image. the other less obvious application is to feature extraction.

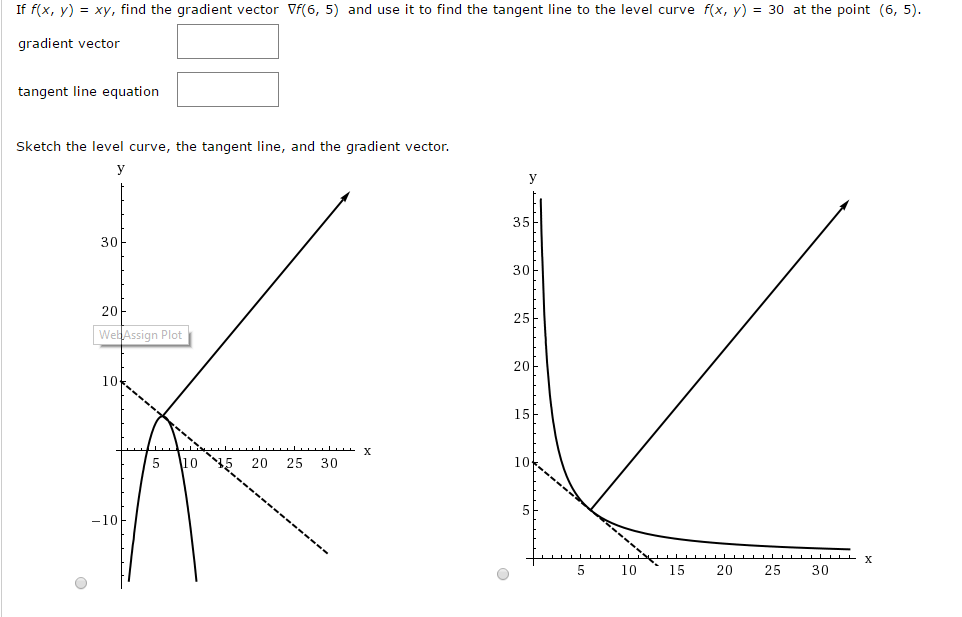
Gradient Vector At Vectorified Collection Of Gradient Vector Free The gradient vector is designed to point in the direction of the greatest initial increase on your curve surface etc. Example 1 find the directional derivative of f (x, y) = 1 2x√y at (3, 4) in the direction of v = h4, −3i. solution. first we compute the partial derivatives: thus. Gradient vector applications 1. suppose fx(2; 4) = 3 and fy(2; 4) = 8. find the directional derivative of f at (2; 4) in the direction of h5; 0i. 2. find a unit vector in the direction in which f(x; y; z) = x2yz increases most rapidly at p (1; 1; 2). what is the rate of increase in this direction? 3. find two unit vectors which are normal to x2. Gradient vector applications the first and most obvious application of gradient vectors is to edge detection. you can see in the gradient images how large gradient values correspond to strong edges in the image. the other less obvious application is to feature extraction.

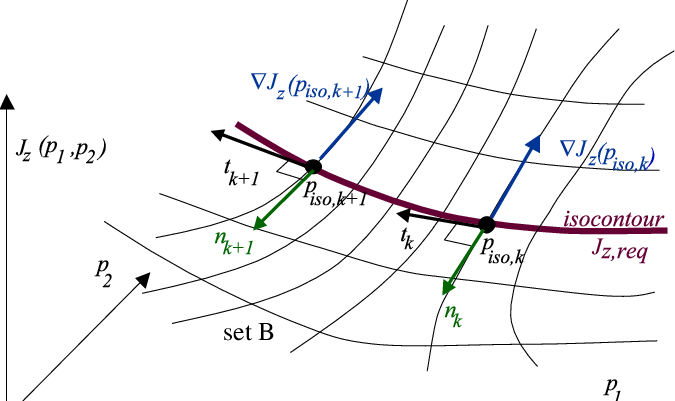
Gradient Vector At Vectorified Collection Of Gradient Vector Free Gradient vector applications 1. suppose fx(2; 4) = 3 and fy(2; 4) = 8. find the directional derivative of f at (2; 4) in the direction of h5; 0i. 2. find a unit vector in the direction in which f(x; y; z) = x2yz increases most rapidly at p (1; 1; 2). what is the rate of increase in this direction? 3. find two unit vectors which are normal to x2. Gradient vector applications the first and most obvious application of gradient vectors is to edge detection. you can see in the gradient images how large gradient values correspond to strong edges in the image. the other less obvious application is to feature extraction.

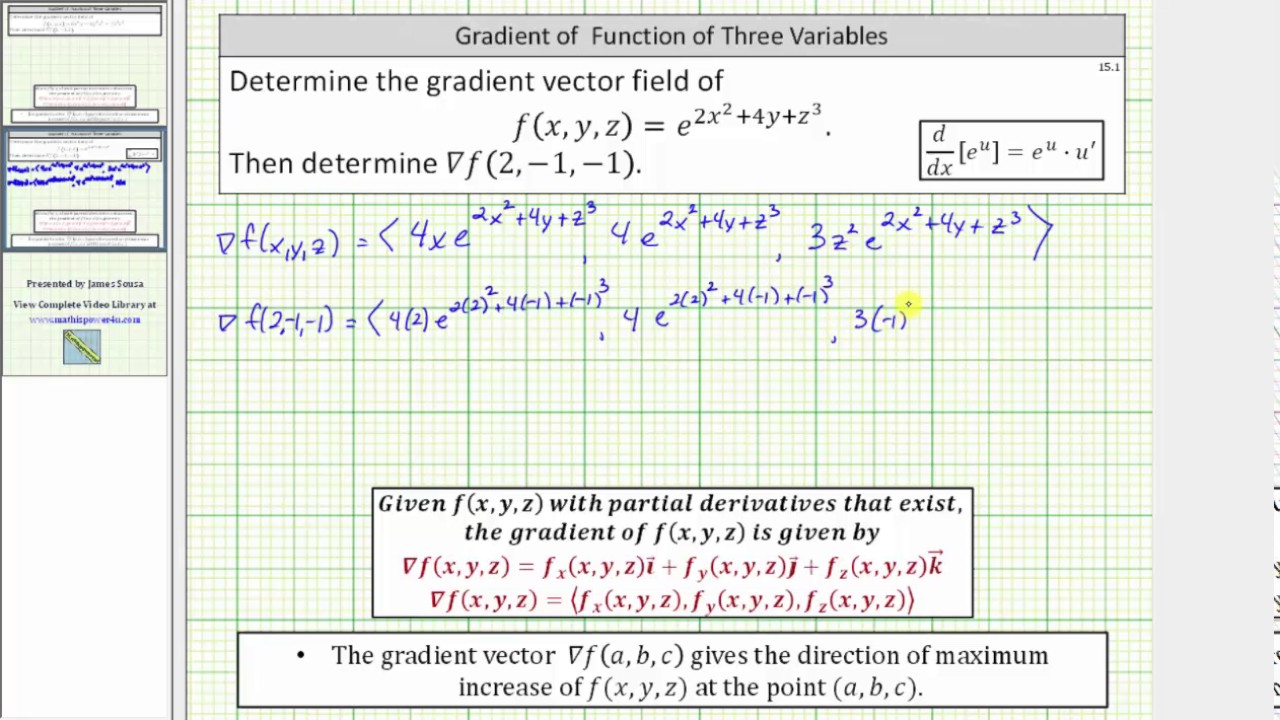
Gradient Vector At Vectorified Collection Of Gradient Vector Free

Step into a world where your Gradient Vector Applications Example 1 passion takes center stage. We're thrilled to have you here with us, ready to embark on a remarkable adventure of discovery and delight.

Gradient Vector Applications Example 1

Gradient Vector Applications Example 1

Gradient Vector Applications Example 1 How to calculate Gradient Vector - Example 1 What Does the Gradient Vector Mean Intuitively? Gradient Vector Application Example 2 Computing the Gradient (Example 1) Gradient Fields (Example 1) gradient applications part 1 Gradient example Gradient Vectors (KristaKingMath) Geometric Meaning of the Gradient Vector How To Find The Directional Derivative and The Gradient Vector Gradient Vector (Field) Example Gradient of straight line Finding the Gradient of a Line virtuallymath.com: gradient vector, simple example Properties of the Gradient Vector Sketching Gradient Fields (Example 1) The Most Useful Calculus 1 Tip! Gradient, Divergence and Curl Concepts | Physics |

Conclusion

Following an extensive investigation, it is unmistakable that article provides informative data in connection with Gradient Vector Applications Example 1. All the way through, the content creator exhibits considerable expertise related to the field. Specifically, the review of important characteristics stands out as particularly informative. The content thoroughly explores how these aspects relate to build a solid foundation of Gradient Vector Applications Example 1.

In addition, the publication stands out in deconstructing complex concepts in an simple manner. This straightforwardness makes the content beneficial regardless of prior expertise. The writer further enriches the review by embedding suitable demonstrations and real-world applications that put into perspective the conceptual frameworks.

An extra component that distinguishes this content is the in-depth research of different viewpoints related to Gradient Vector Applications Example 1. By examining these alternate approaches, the post presents a impartial view of the matter. The exhaustiveness with which the journalist treats the subject is really remarkable and raises the bar for related articles in this field.

In conclusion, this content not only teaches the audience about Gradient Vector Applications Example 1, but also motivates further exploration into this engaging area. Whether you are a novice or a veteran, you will find worthwhile information in this exhaustive content. Thanks for this detailed write-up. If you need further information, do not hesitate to get in touch via the feedback area. I am keen on hearing from you. For further exploration, here are a number of associated articles that are potentially interesting and complementary to this discussion. Enjoy your reading!