27 Tangent Planes And Linear Approximation Download Free Pdf We'll learn about linear approximations in 2d and 3d, and get a formula to memorize to help solve problems involving linear approximations. In this section formally define just what a tangent plane to a surface is and how we use partial derivatives to find the equations of tangent planes to surfaces that can be written as z=f (x,y).

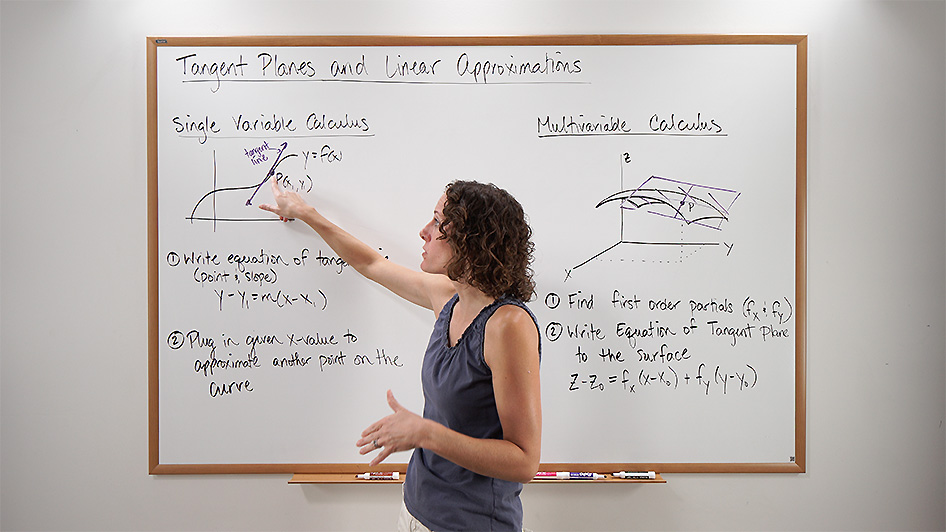
Tangent Planes And Linear Approximations Calcworkshop Tangent planes intuitively, it seems clear that, in a plane, only one line can be tangent to a curve at a point. however, in three dimensional space, many lines can be tangent to a given point. if these lines lie in the same plane, they determine the tangent plane at that point. If you zoom in closely enough to the point where the tangent line is found, the function will appear to be a straight line. near the point, we can take advantage of this by thinking of the tangent line as a linear approximation to the function. Imagine you are standing on a surface that represents the graph of the function f (x, y). if you look around, the surface might be curved, but if you focus on a very small region around your feet, that small region will appear almost flat. this flat region is the tangent plane. Tangent planes and linear approximation 1. let s be the cylinder x2 y2 = 4. find the plane tangent to s at the point (1; p 3; 5). 2. let s be the surface z = y sin x. find the plane tangent to s at the point ;.

Tangent Planes And Linear Approximations Pdf Gradient Tangent Imagine you are standing on a surface that represents the graph of the function f (x, y). if you look around, the surface might be curved, but if you focus on a very small region around your feet, that small region will appear almost flat. this flat region is the tangent plane. Tangent planes and linear approximation 1. let s be the cylinder x2 y2 = 4. find the plane tangent to s at the point (1; p 3; 5). 2. let s be the surface z = y sin x. find the plane tangent to s at the point ;. In the same way that tangent lines played an important role for functions of one variables, tangent planes play an important role for functions of two variables. we rst learn how to derive them. we will then explain why they are important. In this video, i give the formula and use it to find a tangent plane approximation. both the tangent plane and the actual numerical estimate are shown. for more free math videos, visit. We have studied how to represent a surface in parametric form with two parameters using an equation like: for surfaces represented in terms of x,y and z. instead of defining the plane using two tangent to obtain two vectors in the tangent plane we take the partials with respect to u and v to get tangent vectors for each parameter. The analog of a tangent line to a curve is a tangent plane to a surface for functions of two variables. tangent planes can be used to approximate values of functions near known values.