Hyperbolic Functions Pdf Trigonometric Functions Subtraction Why are the partial differential equations so named? i.e, elliptical, hyperbolic, and parabolic. i do know the condition at which a general second order partial differential equation becomes these,. Hyperbolic functions " occur in the solutions of many linear differential equations (for example, the equation defining a catenary), of some cubic equations, in calculations of angles and distances in hyperbolic geometry, and of laplace's equation in cartesian coordinates.

Unleash Hyperbolic Trig Functions Power Beginners Guide I covered hyperbolic trigonometric functions in a recent maths course. however i was never presented with any reasons as to why (or even if) they are useful. is there any good examples of their uses. Is there any formula like this for distance between points in hyperbolic geometry? i know that for example in the poincaré disc model we have a certain formula, another in the klein model, and so on, but i was wondering if we can have some distance formula that exists independent of the model. 5 the hyperbolic functions are defined as the even and odd parts of exp x exp x so exp ±x = cosh x ± sinh x exp ± x = cosh x ± sinh x, in analogy with exp ±ix = cos x ± i sin x exp ± i x = cos x ± i sin x. rearranging gives the desired results. By contrast, in hyperbolic space, a circle of a fixed radius packs in more surface area than its flat or positively curved counterpart; you can see this explicitly, for example, by putting a hyperbolic metric on the unit disk or the upper half plane, where you will compute that a hyperbolic circle has area that grows exponentially with the radius.

Hyperbolic Trig Functions Explained W 15 Examples 5 the hyperbolic functions are defined as the even and odd parts of exp x exp x so exp ±x = cosh x ± sinh x exp ± x = cosh x ± sinh x, in analogy with exp ±ix = cos x ± i sin x exp ± i x = cos x ± i sin x. rearranging gives the desired results. By contrast, in hyperbolic space, a circle of a fixed radius packs in more surface area than its flat or positively curved counterpart; you can see this explicitly, for example, by putting a hyperbolic metric on the unit disk or the upper half plane, where you will compute that a hyperbolic circle has area that grows exponentially with the radius. A way to generate the coordinates in the hyperbolic plane, for each vertex of several cells (polygons) in such a tiling; and the formula to convert those coordinates to the cartesian plane, using the poincare disk model. Hyperbolic functions describe the same thing but can also be used to solve problem that can't be solved by euclidean geometry (where circular functions are sufficient).they can be used to describe euclidean geometry but basically they are extension of it and used to solve problems from non euclidean geometry problems which arise in arise in. A hyperbolic circle turns out to be a euclidean circle after it is flattened out in the poincare half plane model. the only difference is that, since distances are larger nearer to the edge, the center of the hyperbolic circle is not the same as the euclidean center, but is offset toward the edge of the half plane. In the comments we reduced this to integrating 2x, −2y, 0 2 x, 2 y, 0 over the part of paraboloid z =y2 −x2 z = y 2 x 2 that lies within the cylinder x2 y2 = 1 x 2 y 2 = 1. note that the stokes theorem was already used, the rest is just a run of the mill computation of a surface integral. so if you are uncertain about how this is done, that would be the topic to revisit. some points to.

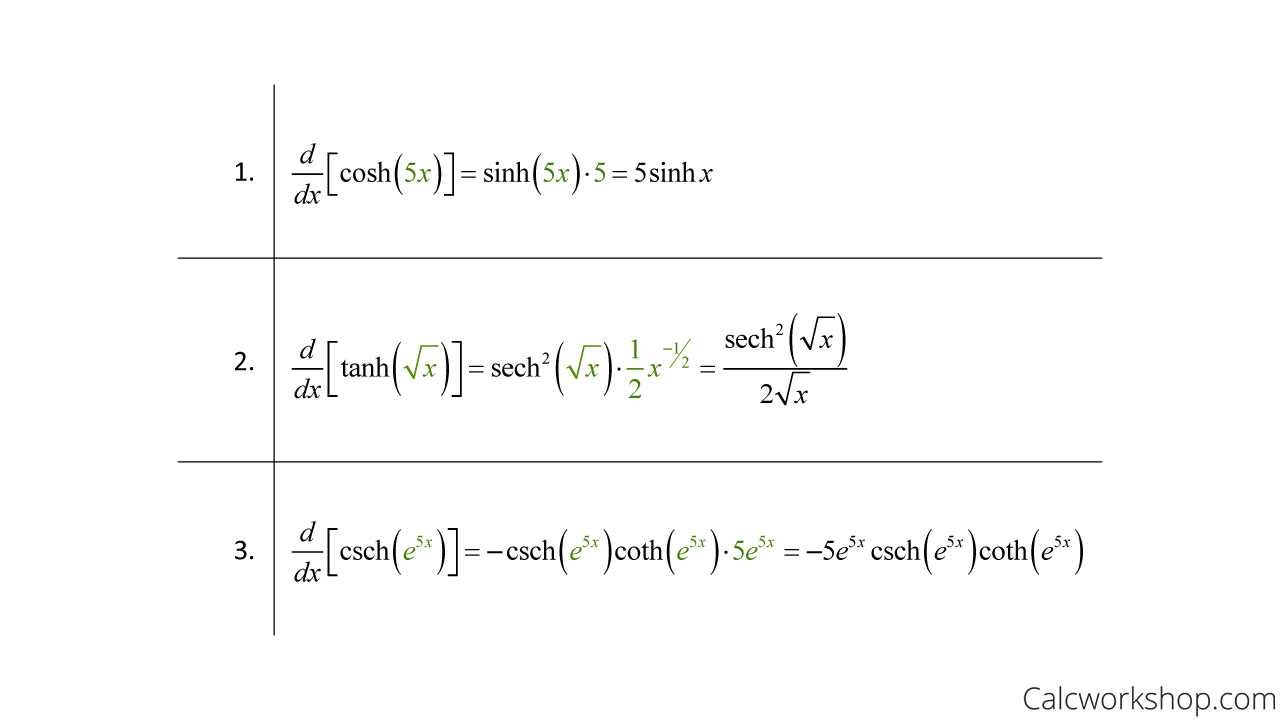
Hyperbolic Trig Functions Explained W 15 Examples A way to generate the coordinates in the hyperbolic plane, for each vertex of several cells (polygons) in such a tiling; and the formula to convert those coordinates to the cartesian plane, using the poincare disk model. Hyperbolic functions describe the same thing but can also be used to solve problem that can't be solved by euclidean geometry (where circular functions are sufficient).they can be used to describe euclidean geometry but basically they are extension of it and used to solve problems from non euclidean geometry problems which arise in arise in. A hyperbolic circle turns out to be a euclidean circle after it is flattened out in the poincare half plane model. the only difference is that, since distances are larger nearer to the edge, the center of the hyperbolic circle is not the same as the euclidean center, but is offset toward the edge of the half plane. In the comments we reduced this to integrating 2x, −2y, 0 2 x, 2 y, 0 over the part of paraboloid z =y2 −x2 z = y 2 x 2 that lies within the cylinder x2 y2 = 1 x 2 y 2 = 1. note that the stokes theorem was already used, the rest is just a run of the mill computation of a surface integral. so if you are uncertain about how this is done, that would be the topic to revisit. some points to.

Hyperbolic Trig Functions Basic Introduction Theorganicchemistrytutor A hyperbolic circle turns out to be a euclidean circle after it is flattened out in the poincare half plane model. the only difference is that, since distances are larger nearer to the edge, the center of the hyperbolic circle is not the same as the euclidean center, but is offset toward the edge of the half plane. In the comments we reduced this to integrating 2x, −2y, 0 2 x, 2 y, 0 over the part of paraboloid z =y2 −x2 z = y 2 x 2 that lies within the cylinder x2 y2 = 1 x 2 y 2 = 1. note that the stokes theorem was already used, the rest is just a run of the mill computation of a surface integral. so if you are uncertain about how this is done, that would be the topic to revisit. some points to.