
Illustration Of Smoothing Images Using Convolution Of Gaussian Filters Download scientific diagram | illustration of smoothing images, using convolution of gaussian filters with the initial image (on the left), and creation of difference of gaussian (dog) from. In these lecture notes we combine the smoothing, i.e. convolution with a gaussian function, and taking the derivative. let ∂ ∂ denote any derivative we want to calculate of the smoothed image: ∂(f ∗gs) ∂ (f ∗ g s).

Illustration Of Smoothing Images Using Convolution Of Gaussian Filters Today: smoothing reduces noise. smoothing reduces noise, giving us (perhaps) a more accurate intensity surface. mask with positive entries that sum to 1. replaces each pixel with an average of its neighborhood. since all weights are equal, it is called a box filter. I learned that gaussian smoothing filters can be described as convolutions. for a 2d image, the formula is: g (x, y) = \omega \ast f (x, y) = \sum {dx= a}^ {a} \sum {dy= b}^ {b} \omega (dx, dy) \cdot f (x dx, y dy) now i am wondering if this is directly transferable to 1d. would the formula look like this?. Image smoothing filters, which include the gaussian, maximum, mean, median, minimum, non local means, percentile, and rank filters, can be applied to reduce the amount of noise in an image. The gaussian smoothing operator is a 2 d convolution operator that is used to `blur' images and remove detail and noise. in this sense it is similar to the mean filter, but it uses a different kernel that represents the shape of a gaussian (`bell shaped') hump.
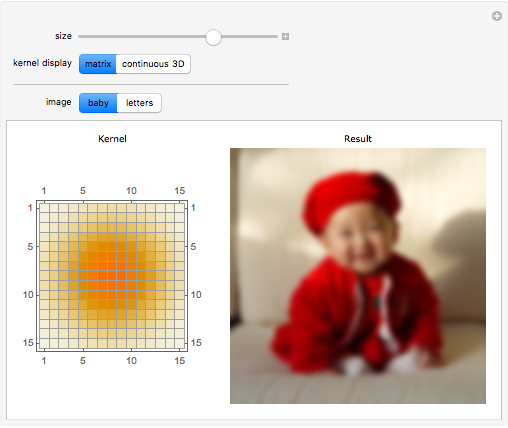
Gaussian Smoothing Wolfram Demonstrations Project Image smoothing filters, which include the gaussian, maximum, mean, median, minimum, non local means, percentile, and rank filters, can be applied to reduce the amount of noise in an image. The gaussian smoothing operator is a 2 d convolution operator that is used to `blur' images and remove detail and noise. in this sense it is similar to the mean filter, but it uses a different kernel that represents the shape of a gaussian (`bell shaped') hump. Convolution is the process to apply a filtering kernel on the image in spatial domain. basic steps are. move over the array with kernel centered at interested point. multiply kernel data with overlapped area. sum or accumulate the output. note : size of output must be same size of input and we need to pad image for not defined pixels. source. Smooth decay to zero rapidly simple analytic formula central limit theorem: limit of applying (most) filters multiple times is some gaussian. This note introduces the concept of convolution in a simplistic but useful way. smoothing is subsequently treated as an important special case. while an image is an array of pixel values, it is often useful to regard it as a sampling of an underlying continuous function of spatial coordinates. A gaussian smoothed image is a single time slice of the solution to the heat equation. anisotropic diffusion uses a variable conductance term for this equation that depends on the structure of the image.