React Native Infinite Scroll Pagination With Flatlist I know that $\\infty \\infty$ is not generally defined. however, if we have 2 equal infinities divided by each other, would it be 1? if we have an infinity divided by another half as big infinity, for. The infinite monkey theorem states that if you have an infinite number of monkeys each hitting keys at random on typewriter keyboards then, with probability 1, one of them will type the complete works of william shakespeare.

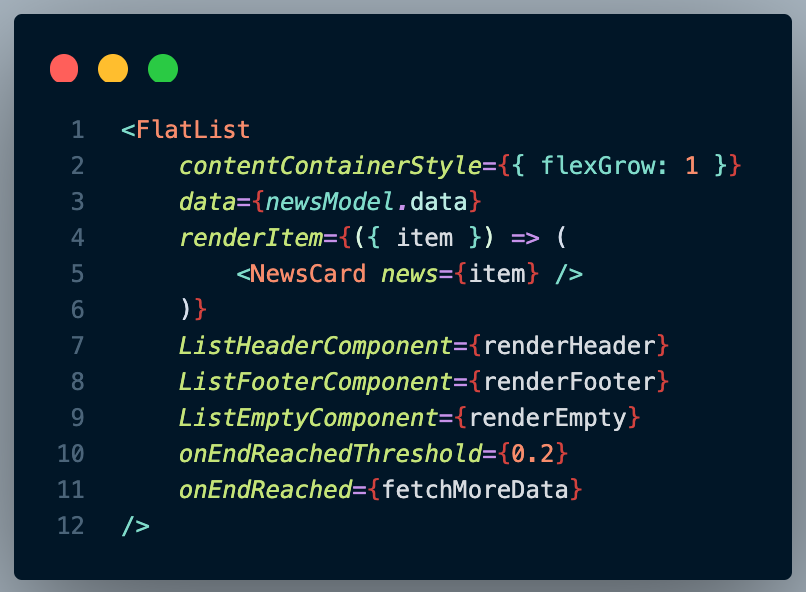
React Native Infinite Scroll Pagination With Flatlist Infinite geometric series formula derivation ask question asked 12 years, 2 months ago modified 4 years, 5 months ago. A set a a is infinite, if it is not finite. the term countable is somewhat ambiguous. (1) i would say that countable and countably infinite are the same. that is, a set a a is countable (countably infinite) if there exists a bijection between a a and n n. (2) other people would define countable to be finite or in bijection with n n. I know that sin(x) sin (x) can be expressed as an infinite product, and i've seen proofs of it (e.g. infinite product of sine function). i found how was euler able to create an infinite product for sinc by using its roots? which discusses how euler might have found the equation, but i wonder how euler could have proved it. The dual space of an infinite dimensional vector space is always strictly larger than the original space, so no to both questions. this was discussed on mo but i can't find the thread.

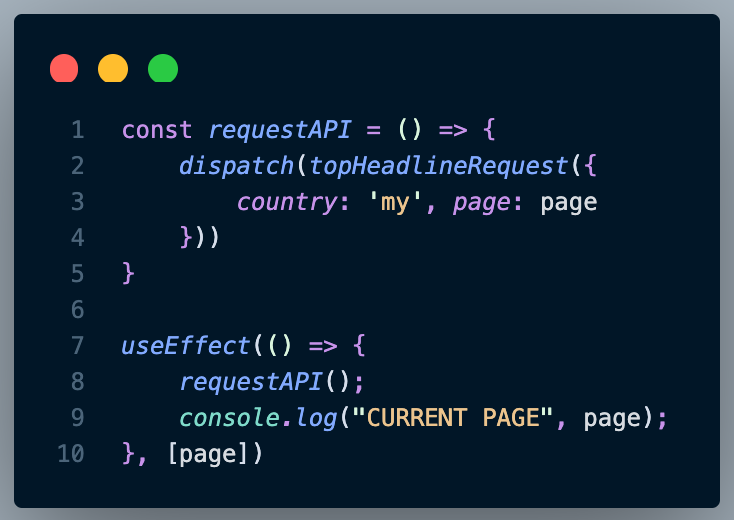
React Native Infinite Scroll Pagination With Flatlist I know that sin(x) sin (x) can be expressed as an infinite product, and i've seen proofs of it (e.g. infinite product of sine function). i found how was euler able to create an infinite product for sinc by using its roots? which discusses how euler might have found the equation, but i wonder how euler could have proved it. The dual space of an infinite dimensional vector space is always strictly larger than the original space, so no to both questions. this was discussed on mo but i can't find the thread. Is this a valid construction of the sequence (xk) (x k)? my knowledge of logic is very limited, but i am concerned that this approach of "infinite" instantiations is not valid. specifically, it feels like i am trying to use an "inductive step", because for any formal finite proof, i obviously could not explicitly construct this sequence. Can you give me an example of infinite field of characteristic p ≠ 0 p ≠ 0? thanks. Not only infinite it's "so big" that there is no infinite set so large as the collection of all types of infinity (in set theoretic terms, the collection of all types of infinity is a class, not a set). you can easily see that there are infinite types of infinity via cantor's theorem which shows that given a set a, its power set p (a) is strictly larger in terms of infinite size (the. Linear transformations on infinite dimensional vector spaces ask question asked 10 years, 5 months ago modified 10 years, 5 months ago.

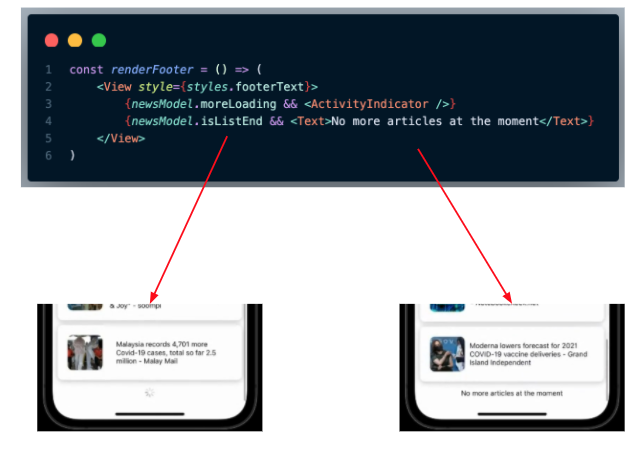
React Native Infinite Scroll Pagination With Flatlist Is this a valid construction of the sequence (xk) (x k)? my knowledge of logic is very limited, but i am concerned that this approach of "infinite" instantiations is not valid. specifically, it feels like i am trying to use an "inductive step", because for any formal finite proof, i obviously could not explicitly construct this sequence. Can you give me an example of infinite field of characteristic p ≠ 0 p ≠ 0? thanks. Not only infinite it's "so big" that there is no infinite set so large as the collection of all types of infinity (in set theoretic terms, the collection of all types of infinity is a class, not a set). you can easily see that there are infinite types of infinity via cantor's theorem which shows that given a set a, its power set p (a) is strictly larger in terms of infinite size (the. Linear transformations on infinite dimensional vector spaces ask question asked 10 years, 5 months ago modified 10 years, 5 months ago.

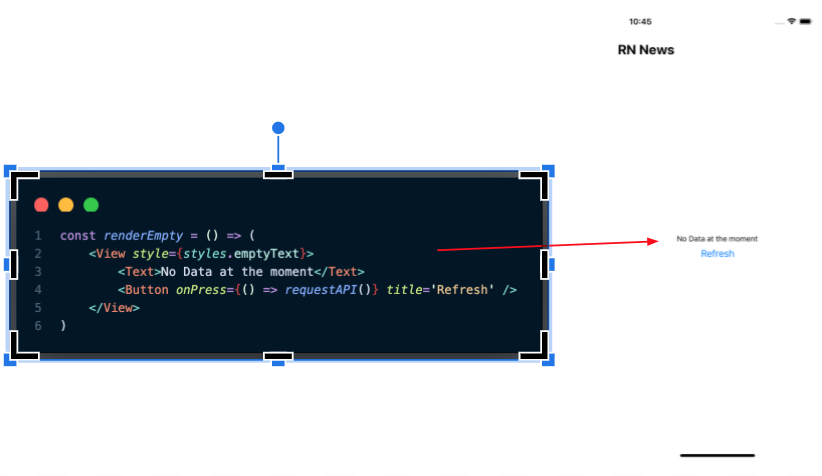
React Native Infinite Scroll Pagination With Flatlist Not only infinite it's "so big" that there is no infinite set so large as the collection of all types of infinity (in set theoretic terms, the collection of all types of infinity is a class, not a set). you can easily see that there are infinite types of infinity via cantor's theorem which shows that given a set a, its power set p (a) is strictly larger in terms of infinite size (the. Linear transformations on infinite dimensional vector spaces ask question asked 10 years, 5 months ago modified 10 years, 5 months ago.