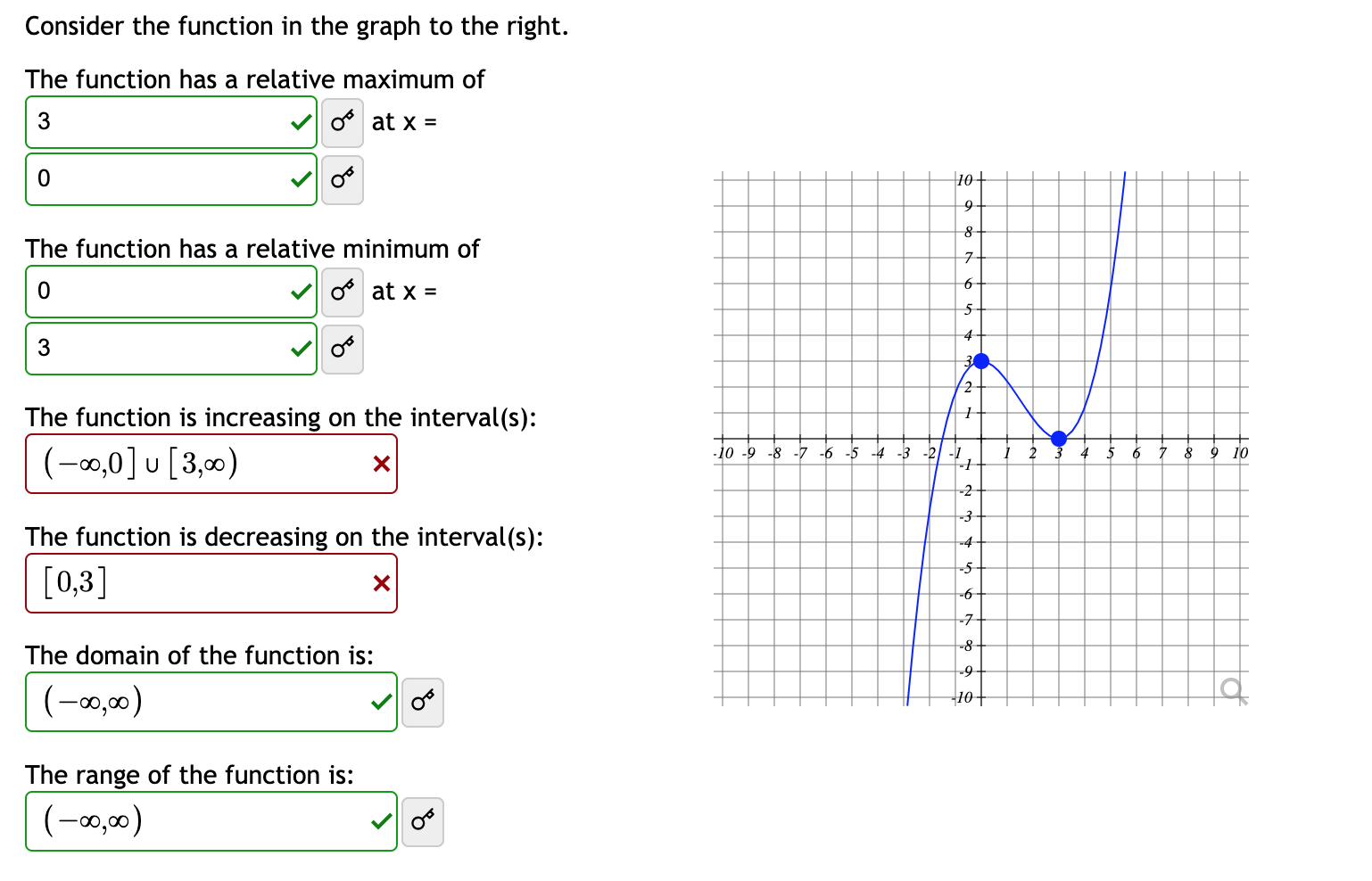
Solved Consider The Function In The Graph To The Right The Chegg A relative maximum point on a function is a point (x,y) (x, y) on the graph of the function whose y y coordinate is larger than all other y y coordinates on the graph at points “close to” (x,y). (x, y) more precisely, (x,f (x)) (x, f (x)) is a relative maximum if there is an interval (a,b) (a, b) with a

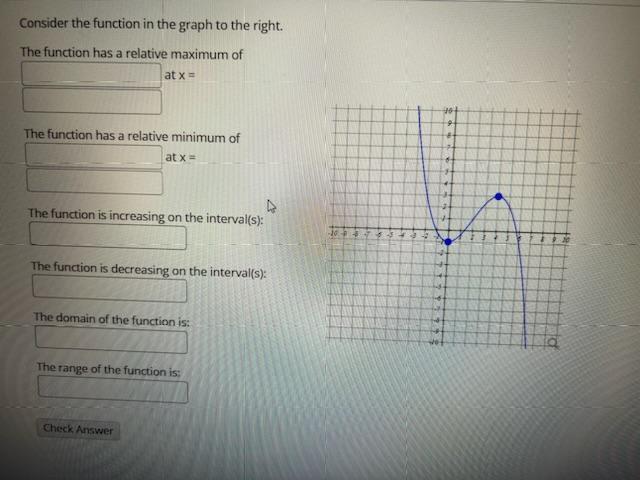
Solved Consider The Function In The Graph To The Right The Chegg Question: consider the function graphed below. je 10 a. the function has a relative maximum of at x = b. the function has a relative minimum of at x = c. the function is increasing on the interval (s): d. the function is decreasing on the interval (s): e. the domain of the function is: f. the range of the function is: please explain and check. We call it a "relative" maximum because other values of the function may in fact be greater. we say that a function f (x) has a relative minimum value at x = b, if f (b) is less than any value immediately preceding or follwing. again, other values of the function may in fact be less. with that understanding, then, we will drop the term relative. Find the x coordinate of the relative maximum on the interval (−5, 0). to find relative maximums, we need to find where our first derivative changes sign. to do this, find your first derivative and then find where it is equal to zero. begin with: g(x) =x3 4x2. g′(x) = 3x2 8x. g′(x) = x(3x 8) g′(x) = 0 at x = 0, x = −8 3. How do i find relative minimum & maximum points with differential calculus? a relative maximum point is a point where the function changes direction from increasing to decreasing (making that point a "peak" in the graph).

Solved Consider The Function In The Graph To The Right The Chegg Find the x coordinate of the relative maximum on the interval (−5, 0). to find relative maximums, we need to find where our first derivative changes sign. to do this, find your first derivative and then find where it is equal to zero. begin with: g(x) =x3 4x2. g′(x) = 3x2 8x. g′(x) = x(3x 8) g′(x) = 0 at x = 0, x = −8 3. How do i find relative minimum & maximum points with differential calculus? a relative maximum point is a point where the function changes direction from increasing to decreasing (making that point a "peak" in the graph). A function f has a relative maximum at x = c if there exists an open interval (a, b) containing c such that f (c) ≥ f (x) for all x in (a, b). in this case, f (c) is called a relative maximum value of f. Video answer: so in this problem, we're given the graph of a function. so in part a, we want to find the relative max. well, the relative max occurs at the highest point that you can see or your function. it doesn't necessarily mean it's that. Likewise, a function f f has an absolute minimum at x = b x = b if f(b) ≤ f(x) f (b) ≤ f (x) for all x x in the domain of f f. if f f has more than one local absolute maximum, we call the collection of these maximums the absolute maxima. This calculus video tutorial explains how to find the local maximum and minimum values of a function. in order to determine the relative extrema, you need t.