Quantum Mechanics Help Normalizing A Wave Function Physics Stack It is important to demonstrate that if a wavefunction is initially normalized then it stays normalized as it evolves in time according to schrödinger’s equation. Normalization of the wavefunction a probability is a real number between 0 and 1, inclusive. an outcome of a measurement which has a probability 0 is an impossible outcome, whereas an outcome which has a probability 1 is a certain outcome.

Quantum Mechanics Normalizing 3 Dimensional Wave Function Physics In quantum mechanics, it's always important to make sure the wave function you're dealing with is correctly normalized. in this video, we will tell you why this is important and also how to. Normalization of the wavefunction now, a probability is a real number between 0 and 1. an outcome of a measurement which has a probability 0 is an impossible outcome, whereas an outcome which has a probability 1 is a certain outcome. according to eq. (), the probability of a measurement of yielding a result between and is. The above equation is called the normalization condition. once we have a solution ψ (x) to the schrodinger equation, this condition can be used to set the overall amplitude of the wave function ψ. Normalising a wave function simply means multiplying it by a constant to ensure that the sum of the probabilities for finding that particle equals 1. mathematically, this means integrating over all space should equal 1. consider a simple wave function, operating between the limits .

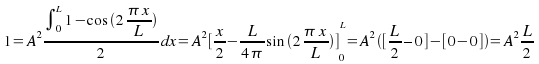
Normalizing The Wavefunction The above equation is called the normalization condition. once we have a solution ψ (x) to the schrodinger equation, this condition can be used to set the overall amplitude of the wave function ψ. Normalising a wave function simply means multiplying it by a constant to ensure that the sum of the probabilities for finding that particle equals 1. mathematically, this means integrating over all space should equal 1. consider a simple wave function, operating between the limits . Normalization is to minimize the redundancy and remove insert, update and delete anomaly. it divides larger tables into smaller tables and links them using relationships. Normalization of the wave function is a fundamental concept in quantum mechanics. it refers to the process of ensuring that the total probability of finding a particle in any location is equal to one. this is achieved by dividing the wave function by a normalization constant. The quantum state of a system |ψ | ψ must always be normalized: ψ|ψ = 1 ψ | ψ = 1. since the wave function of a system is directly related to the wave function: ψ(p) = p|ψ ψ (p) = p | ψ , it must also be normalized. otherwise, the calculations of observables won't come out right. Figure i: a wavepacket ψ(x) in position space or φ(k) in momentum space whose wavefunction for large x (or k) falls off faster than x−1 2 (k−1 2) can be directly normalized.

Need Help On Normalizing Wavefunction Question R Chemhelp Normalization is to minimize the redundancy and remove insert, update and delete anomaly. it divides larger tables into smaller tables and links them using relationships. Normalization of the wave function is a fundamental concept in quantum mechanics. it refers to the process of ensuring that the total probability of finding a particle in any location is equal to one. this is achieved by dividing the wave function by a normalization constant. The quantum state of a system |ψ | ψ must always be normalized: ψ|ψ = 1 ψ | ψ = 1. since the wave function of a system is directly related to the wave function: ψ(p) = p|ψ ψ (p) = p | ψ , it must also be normalized. otherwise, the calculations of observables won't come out right. Figure i: a wavepacket ψ(x) in position space or φ(k) in momentum space whose wavefunction for large x (or k) falls off faster than x−1 2 (k−1 2) can be directly normalized.

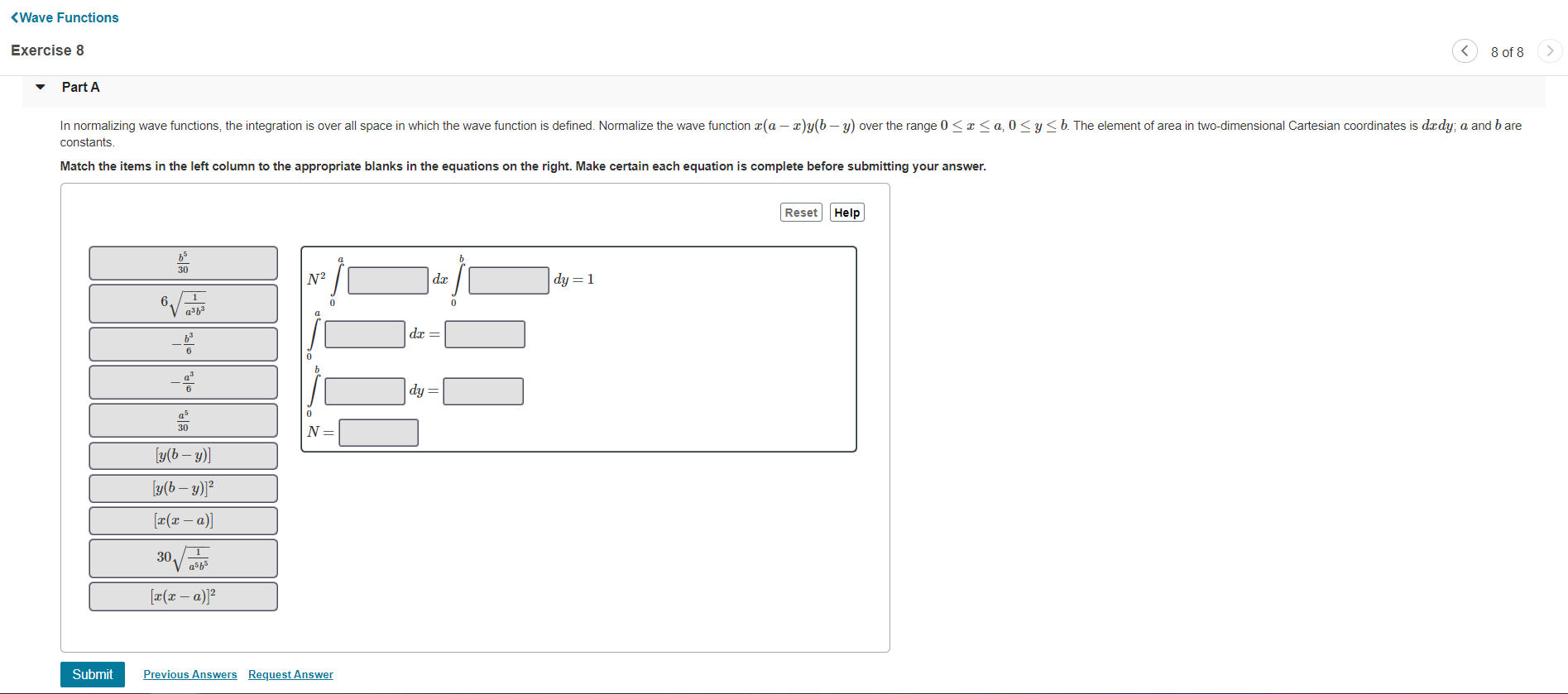
Solved Part A In Normalizing Wave Functions The Chegg The quantum state of a system |ψ | ψ must always be normalized: ψ|ψ = 1 ψ | ψ = 1. since the wave function of a system is directly related to the wave function: ψ(p) = p|ψ ψ (p) = p | ψ , it must also be normalized. otherwise, the calculations of observables won't come out right. Figure i: a wavepacket ψ(x) in position space or φ(k) in momentum space whose wavefunction for large x (or k) falls off faster than x−1 2 (k−1 2) can be directly normalized.