
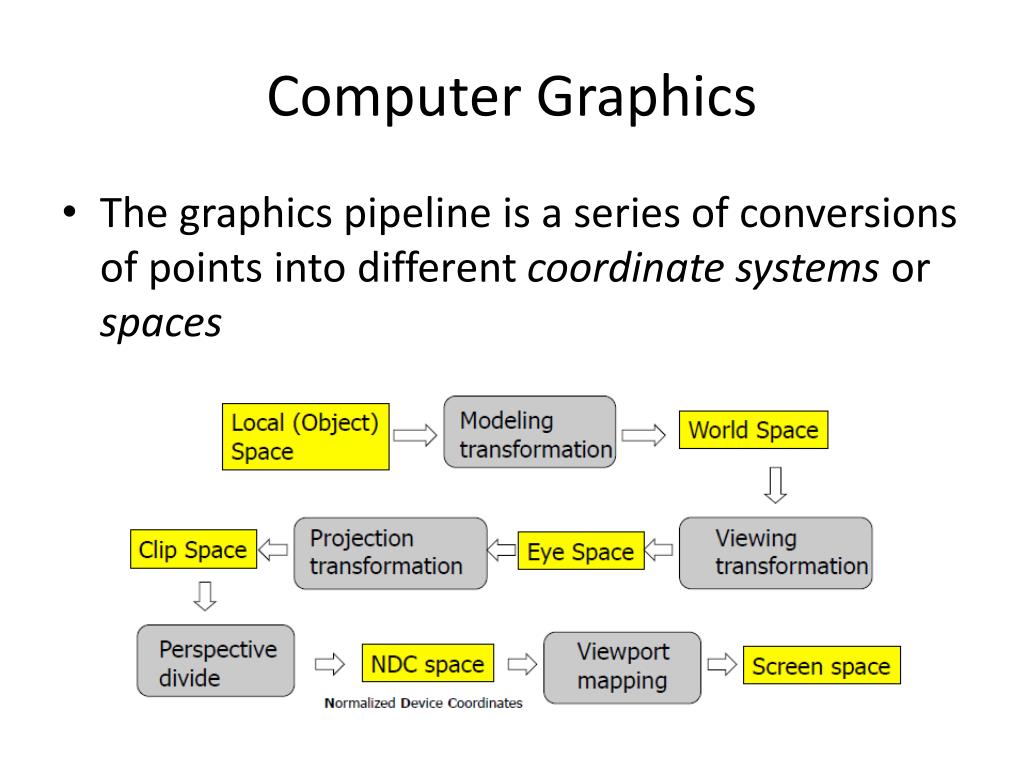
Computer Graphics Transformations An Introduction To 2d This document discusses 2d geometric transformations including translation, rotation, and scaling. it provides the mathematical definitions and matrix representations for each transformation. Computer graphics programming: matrices and transformations cse 3451 matt boggus outline • computer graphics overview • types of 3d modeling • solid • shell boundary • unity mesh objects.
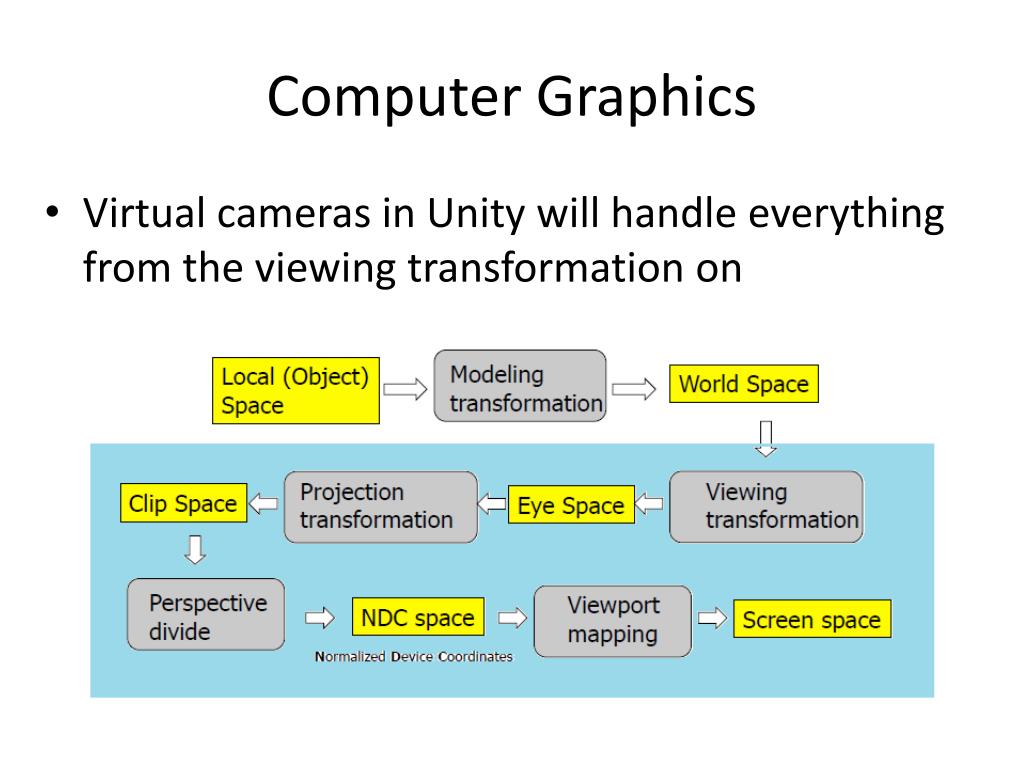
Ppt Computer Graphics Programming Matrices And Transformations What you should get: by expressing the transformations with homogenous equations and coordinates, all transformations can be expressed as matrix multiplications. Objectives introduce standard transformations rotation translation scaling shear derive homogeneous coordinate transformation matrices learn to build arbitrary transformation matrices from simple transformations general transformations a transformation maps points to other points and or vectors to other vectors affine transformations line. With homogeneous coordinates, we can represent all 2d affine transformations as 3d linear transformations. With homogeneous coordinates, we can represent all 2d affine transformations as 3d linear transformations. we can then use matrix multiplication to transform objects.
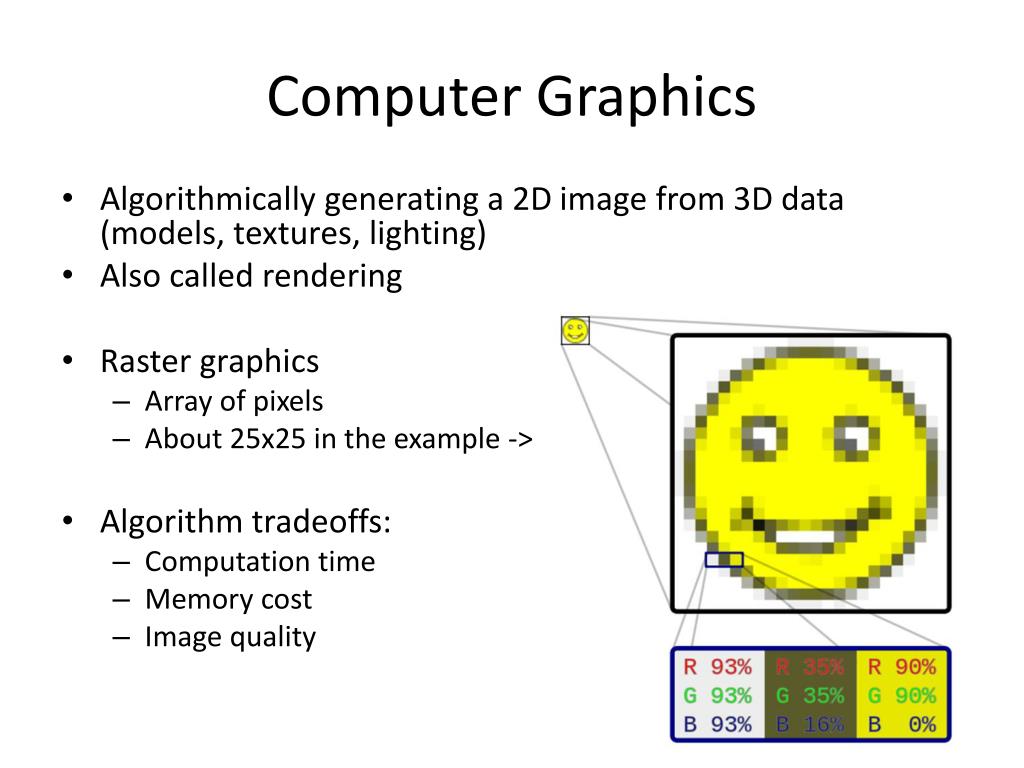
Ppt Computer Graphics Programming Matrices And Transformations With homogeneous coordinates, we can represent all 2d affine transformations as 3d linear transformations. With homogeneous coordinates, we can represent all 2d affine transformations as 3d linear transformations. we can then use matrix multiplication to transform objects. Basic transformations translation: rotation: scaling: homogeneous transform advantages unified view of transformation as matrix multiplication easier in hardware and software to compose transformations, simply multiply matrices order matters: ab is generally not the same as ba allows for non affine transformations: perspective projections!. This document discusses various types of geometric transformations used in computer graphics. it describes transformation as a change in orientation, size, or shape of an object. What you should get: by expressing the transformations with homogenous equations and coordinates, all transformations can be expressed as matrix multiplications. Current transformation matrix (ctm) conceptually there is a 4x4 homogeneous coordinate matrix, the current transformation matrix (ctm), that is part of the state and is applied to all vertices that pass down the pipeline.
Ppt Computer Graphics Programming Matrices And Transformations Basic transformations translation: rotation: scaling: homogeneous transform advantages unified view of transformation as matrix multiplication easier in hardware and software to compose transformations, simply multiply matrices order matters: ab is generally not the same as ba allows for non affine transformations: perspective projections!. This document discusses various types of geometric transformations used in computer graphics. it describes transformation as a change in orientation, size, or shape of an object. What you should get: by expressing the transformations with homogenous equations and coordinates, all transformations can be expressed as matrix multiplications. Current transformation matrix (ctm) conceptually there is a 4x4 homogeneous coordinate matrix, the current transformation matrix (ctm), that is part of the state and is applied to all vertices that pass down the pipeline.