
Probability Powerpoint Lesson Pdf Probability Probability And This document outlines probability density functions (pdfs) including: the definition of a pdf as describing the relative likelihood of a random variable taking a value. properties of pdfs such as being nonnegative and integrating to 1. joint pdfs describing the probability of multiple random variables taking values simultaneously. 3 probability density function we use probability density function f (x) to represent the distribution of a continuous r.v. the value of f (x) is not a probability. instead, the integral of f (x) gives the required probability. several important properties can identify a p.d.f. 4 properties of p.d.f. f (x) ? 0 5 ex. of p.d.f. ex. (p.71 q.2).

Ppt Probability Density Functions Powerpoint Presentation Free Review the fundamental concepts of probability. understand the difference between discrete and continuous random variable. review the most common probability models. overview. probability and random variables. random experiment and random variable. probability mass density functions. expectation, variance, covariance, correlation. A (probability) density function f (x) for a random variable x is a continuous function that satisfies three properties: (1) the function outputs must be >0, that is, the graph of the function cannot go below the x axis; (2) the total area between the graph of the function and the horizontal axis is 1; (3) the probability values for x. Probability and probability density functions. a random variable x is a variable whose numerical value depends on chance. for example, what is the probability that a patient’s recovery time (x) is between 40 min and 50 min? what proportion of patient recovery times (x) are less than 60 min?. Slideserve has a very huge collection of probability density functions powerpoint presentations. you can view or download probability density functions presentations for your school assignment or business presentation.
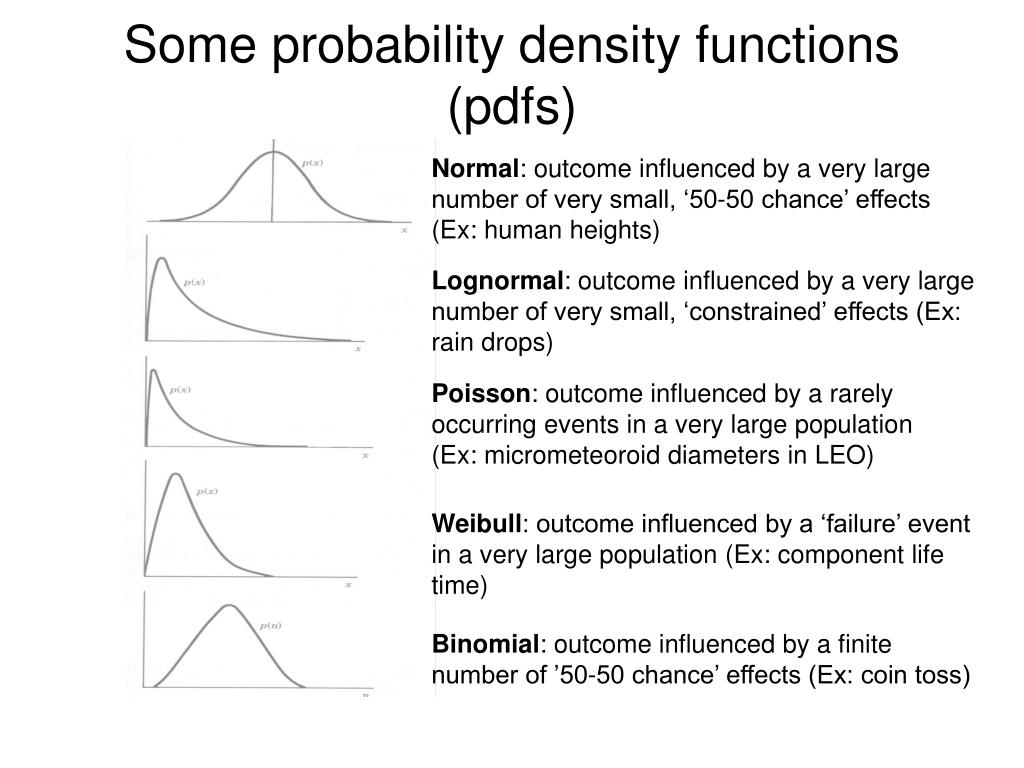
Ppt Some Probability Density Functions Pdfs Powerpoint Presentation Probability and probability density functions. a random variable x is a variable whose numerical value depends on chance. for example, what is the probability that a patient’s recovery time (x) is between 40 min and 50 min? what proportion of patient recovery times (x) are less than 60 min?. Slideserve has a very huge collection of probability density functions powerpoint presentations. you can view or download probability density functions presentations for your school assignment or business presentation. Probability density functions let’s consider the temperature example again. we want to know the probability that the temperature is in any given interval. for example, what’s the probability for the temperature between 70 and 80 ? ultimately, we want to know the probability distribution for x . Probability and probability density functions. a random variable x is a variable whose numerical value depends on chance. for example, what is the probability that a patient’s recovery time ( x ) is between 40 min and 50 min?. For a continuous r.v.𝑋, a probability𝑝(𝑋 = 𝑥) or 𝑝(𝑥) is meaningless. for cont. r.v., we talk in terms of prob. within an interval𝑋 ∈(𝑥,𝑥 𝛿𝑥) . 𝑝(𝑥)𝛿𝑥 is the prob. that 𝑋 ∈(𝑥,𝑥 𝛿𝑥) as 𝛿𝑥→0. 𝑝(𝑥) is the probability density at 𝑋= 𝑥. 𝑝𝑥≥0. 𝑝𝑥≤ 1. 𝑝𝑥𝑑𝑥=1. discrete example: roll of a die. x. p(x) 1 6. 4. The concept of discrete random variable and its associated probability distribution is extended to continuous sample spaces. we can describe continuous random variables and connect with these probability density functions.
Probability Density Powerpoint Templates Slides And Graphics Probability density functions let’s consider the temperature example again. we want to know the probability that the temperature is in any given interval. for example, what’s the probability for the temperature between 70 and 80 ? ultimately, we want to know the probability distribution for x . Probability and probability density functions. a random variable x is a variable whose numerical value depends on chance. for example, what is the probability that a patient’s recovery time ( x ) is between 40 min and 50 min?. For a continuous r.v.𝑋, a probability𝑝(𝑋 = 𝑥) or 𝑝(𝑥) is meaningless. for cont. r.v., we talk in terms of prob. within an interval𝑋 ∈(𝑥,𝑥 𝛿𝑥) . 𝑝(𝑥)𝛿𝑥 is the prob. that 𝑋 ∈(𝑥,𝑥 𝛿𝑥) as 𝛿𝑥→0. 𝑝(𝑥) is the probability density at 𝑋= 𝑥. 𝑝𝑥≥0. 𝑝𝑥≤ 1. 𝑝𝑥𝑑𝑥=1. discrete example: roll of a die. x. p(x) 1 6. 4. The concept of discrete random variable and its associated probability distribution is extended to continuous sample spaces. we can describe continuous random variables and connect with these probability density functions.