Probability Density Function Data Science Learning Keystone What is the intuition behind the probability density function of a continuous random variable? integrating it within two points provides the probability that is associated between two points, but if you plug a single value into f(x = x) f (x = x), it outputs a value. But only and precisely the red line is a probability function, or more specifically, a probability density function. don't stress too much about what exactly is the definition for "probability measure" "probability distribution".

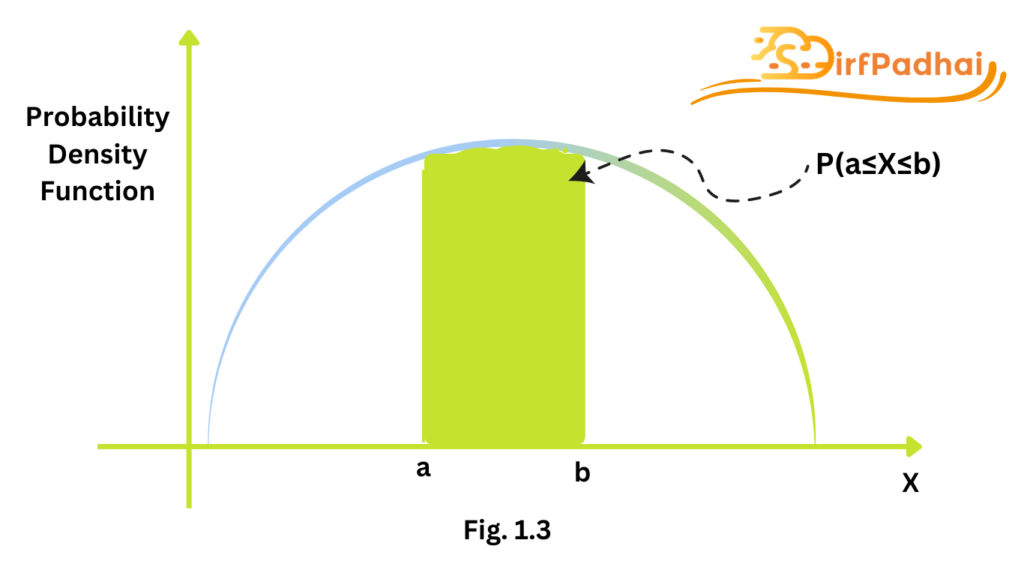
Probability Density Function Machine Learning Sirf Padhai The probability density function (pdf) is indeed referring to the density of a probability measure, so these are the same thing. you should bear in mind that the density is formally defined as the radon nikodym derivative of the probability measure with respect to a dominating measure. A bounded function in mathematics is always (1), but we don't know in what context you found this. as an example for an unbounded probability density, take the with either α <1 α <1 or β <1 β <1 or both. Histogram density estimator is estimating the density with a sum of piecewise functions (density of a uniform). kde is using a sum of smooth function (gaussian is an example) (as long as they are positive they can be transformed into a density by normalization) the use of " mixture " in statistic is about convex combination of densities. Could you please explain to me why the probability density function of a sine wave looks like it does, i.e. like a basket with the greatest probability density located at 1 and 1 points, decreasing towards the centre? since each value appears twice over one period of the sine wave, wouldn't the probability of each value be the same?.

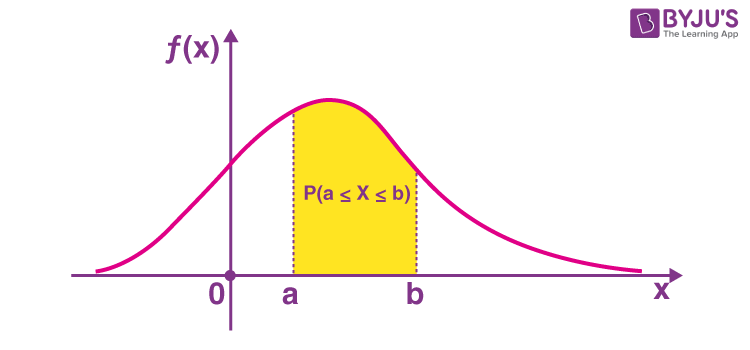
Probability Density Function Histogram density estimator is estimating the density with a sum of piecewise functions (density of a uniform). kde is using a sum of smooth function (gaussian is an example) (as long as they are positive they can be transformed into a density by normalization) the use of " mixture " in statistic is about convex combination of densities. Could you please explain to me why the probability density function of a sine wave looks like it does, i.e. like a basket with the greatest probability density located at 1 and 1 points, decreasing towards the centre? since each value appears twice over one period of the sine wave, wouldn't the probability of each value be the same?. How does a computer algorithm set up to take as input an arbirary bivariate probability density function, generate pairs of numbers from that distribution? i have found a routine called simcontour. A probability density function (pdf) is a non negative function that integrates to 1 1. the likelihood is defined as the joint density of the observed data as a function of the parameter. My goal is to create a function, from which i could do a further calculation to find the probability that a value would fall within a certain range. for example, find out what is the probability of values between −5 5 to −4.5 4.5 in data. A mode of a continuous probability distribution is a value at which the probability density function (pdf) attains its maximum value so given a specific definition of the mode you find it as you would find that particular definition of "highest value" when dealing with functions more generally, (assuming that the distribution is unimodal under.

Probability Density Function How does a computer algorithm set up to take as input an arbirary bivariate probability density function, generate pairs of numbers from that distribution? i have found a routine called simcontour. A probability density function (pdf) is a non negative function that integrates to 1 1. the likelihood is defined as the joint density of the observed data as a function of the parameter. My goal is to create a function, from which i could do a further calculation to find the probability that a value would fall within a certain range. for example, find out what is the probability of values between −5 5 to −4.5 4.5 in data. A mode of a continuous probability distribution is a value at which the probability density function (pdf) attains its maximum value so given a specific definition of the mode you find it as you would find that particular definition of "highest value" when dealing with functions more generally, (assuming that the distribution is unimodal under.

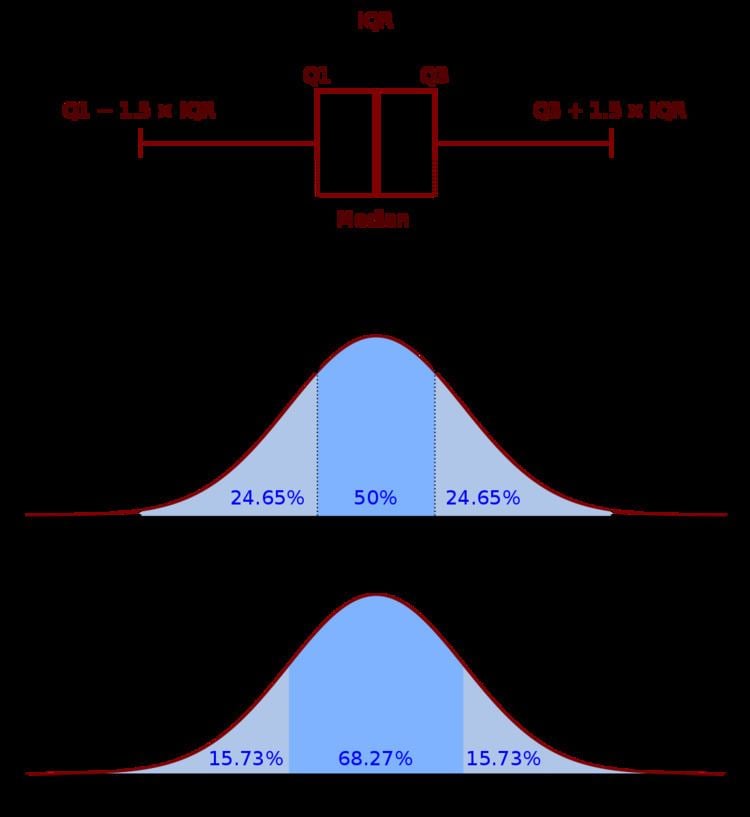
Probability Density Function Alchetron The Free Social Encyclopedia My goal is to create a function, from which i could do a further calculation to find the probability that a value would fall within a certain range. for example, find out what is the probability of values between −5 5 to −4.5 4.5 in data. A mode of a continuous probability distribution is a value at which the probability density function (pdf) attains its maximum value so given a specific definition of the mode you find it as you would find that particular definition of "highest value" when dealing with functions more generally, (assuming that the distribution is unimodal under.