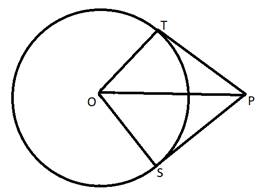
Prove That The Lengths Of Tangents Drawn From An External Point To A Given: let circle be with centre o and p be a point outside circle pq and pr are two tangents to circle intersecting at point q and r respectively to prove: lengths of tangents are equal i.e. pq = pr construction: join oq , or and op proof: as pq is a tangent oq ⊥ pq so, ∠ oqp = 90° hence Δ oqp is right triangle similarly, pr is a tangent. To prove: the lengths of tangents drawn from an external point to a circle are equal. let pq and pr be the two tangents drawn to the circle of centre o as shown in the figure. construction. now ∆por and ∆poq. in order to prove they have the same length, we will first prove that both triangles are similar.

Math Labs With Activity The Lengths Of The Tangents Drawn From An Tp and tq are two tangents drawn from an external point t to the circle c (o, r). to prove: tp = tq. construction: join ot. proof: we know that a tangent to the circle is perpendicular to the radius through the point of contact. ∴ ∠opt = ∠oqt = 90°. in Δopt and Δoqt, ot = ot (common) op = oq (radius of the circle) ∠opt = ∠oqt (90°). Q) prove that the lengths of tangents drawn from an external point to a circle are equal. using above result, find the length bc of Δ abc. given that, a circle is inscribed in Δ abc touching the sides ab, bc and. ca at r, p and q respectively and ab= 10 cm, aq= 7cm ,cq= 5cm. ans: (i) tangent equal from an external point:. To verify that the lengths of the tangents drawn from an external point to a circle are equal. materials required. the theorem can be proved as follows. let two tangents ap and aq be drawn from a point a (external point) to a circle with its centre at o and having a radius r. join op, oq and oa. Prove that the length of the tangents drawn from an external point to a circle are equal. 1. draw the diagram: let p be an external point from which two tangents pa and pb are drawn to the circle, touching the circle at points a and b, respectively. 2. identify the tangents and radii:.

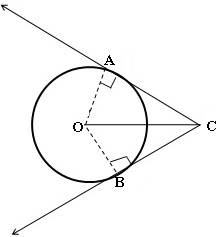
Prove That The Lengths Of Tangents Drawn From An External Point To A To verify that the lengths of the tangents drawn from an external point to a circle are equal. materials required. the theorem can be proved as follows. let two tangents ap and aq be drawn from a point a (external point) to a circle with its centre at o and having a radius r. join op, oq and oa. Prove that the length of the tangents drawn from an external point to a circle are equal. 1. draw the diagram: let p be an external point from which two tangents pa and pb are drawn to the circle, touching the circle at points a and b, respectively. 2. identify the tangents and radii:. Theorem: exactly two tangents can be drawn from an exterior point to a given circle. consider the following figure, in which a tangent has been drawn from an exterior point p to a circle s (with center o), and the point of contact is a: we will make use of the fact that ∠p ao ∠ p a o must be 90 degrees. Given: a circle with centre o; pa and pb are two tangents to the circle drawn from an external point p. to prove: pa = pb. construction: join oa, ob, and op. it is known that a tangent at any point of a circle is perpendicular to the radius through the point of contact. o a ⊥ p a. o b ⊥ p b. in triangle opa and opb. ∠ o p a = ∠ o p b. Given, tp and tq are two tangent drawn from an external point t to the circle c (o, r). to prove: tp = tq construction: join ot. proof: we know that a tangent to the circle is perpendicular to the radius through the point of contact. ∴ ∴ ∠opt = ∠oqt = 90° in op t o p t and oqt o q t, ot = ot (common) op = oq (radius of the circle). Here we will prove that from any point outside a circle two tangents can be drawn to it and they are equal in length. given: o is the centre of a circle and t is a point outside the circle. construction: join o and t. draw a circle with to as diameter which cuts the given circle at m and n. join t to m and n.