End Behavior Polynomial Functions Foldable Notes And Maze This resource is a one page explanation of polynomial end behavior. students have expressed over and over how helpful this resource is to understanding end behavior. reported resources will be reviewed by our team. report this resource to let us know if this resource violates tpt’s content guidelines. Determine the end behavior by describing the leading coefficent and degree. state whether odd even degree and positive negative leading coefficient. f (x) = x4 2x2 2x 1. f (x) = x2 8x 12. f (x) = x2 2x 1. f (x) = x3 4x2 3. f (x) = x2 4x 5. f (x) = x2 3. f (x) = x2 8x 10. f (x) = x5 4x3 3x 3.

1 7 Polynomial End Behavior Filled In Pdf Zero Of A Function The end behavior of a polynomial function describes how the graph behaves as x approaches ∞ or ∞. in other words, it indicates the direction in which the ‘tails’ of the graph extend as the input value (x) becomes extremely large (x → ∞) or extremely small (x → −∞). Explain below how knowing the degree and leading coefficient of a polynomial can help you determine the end behavior. use a complete sentence. This worksheet will guide you through looking at the end behaviors of several polynomial functions. at the end, we will generalize about all polynomial functions. Given the equation of a polynomial function, we can analyze the degree and leading coefficient of the polynomial. determine if the degree of the following function is even or odd and if the leading coefficient is positive or negative.

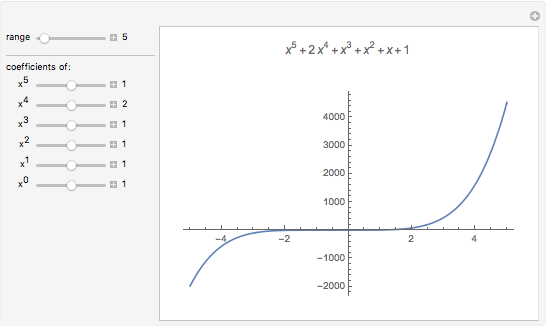
End Behavior Of Polynomial Functions Wolfram Demonstrations Project This worksheet will guide you through looking at the end behaviors of several polynomial functions. at the end, we will generalize about all polynomial functions. Given the equation of a polynomial function, we can analyze the degree and leading coefficient of the polynomial. determine if the degree of the following function is even or odd and if the leading coefficient is positive or negative. End behavior and zeroes of polynomials. describe the end behavior of the graph of the polynomial function. use a graphing calculator to verify your result. third degree polynomial with two real zeros and a negative leading coefficient. fourth degree polynomial with two real zeros and a positive leading coefficient. C) what is the leading coefficient? d) classify the leading coefficient as positive or negative. e) describe the end behavior in words. f) describe the end behavior using symbols. g) use the graphing calculator to sketch the general shape of the graph. 1) f (x) = −x5 3x3 − 2x − 1 2) f (x) = −x5 3x3 − 3x. Describe the end behavior of each function. f ( x ) → −∞ as x → −∞. Graph the following function and describe the increasing decreasing intervals. = ! − 4 2.

Reference Sheet End Behavior Of Polynomial Functions By Math With Ms Ship End behavior and zeroes of polynomials. describe the end behavior of the graph of the polynomial function. use a graphing calculator to verify your result. third degree polynomial with two real zeros and a negative leading coefficient. fourth degree polynomial with two real zeros and a positive leading coefficient. C) what is the leading coefficient? d) classify the leading coefficient as positive or negative. e) describe the end behavior in words. f) describe the end behavior using symbols. g) use the graphing calculator to sketch the general shape of the graph. 1) f (x) = −x5 3x3 − 2x − 1 2) f (x) = −x5 3x3 − 3x. Describe the end behavior of each function. f ( x ) → −∞ as x → −∞. Graph the following function and describe the increasing decreasing intervals. = ! − 4 2.

Reference Sheet End Behavior Of Polynomial Functions By Math With Ms Ship Describe the end behavior of each function. f ( x ) → −∞ as x → −∞. Graph the following function and describe the increasing decreasing intervals. = ! − 4 2.

End Behavior Of Polynomial Functions Fill Online Printable Fillable