Funciones Inyectiva Sobreyectiva Biyectiva Y Inversa 2023 2 Pdf 51 k 3 funciones regla que se le asocia a cada numero "x" de junto "b un conjunto "a" un unico valor f (x) de un con f (x)=2x 1 3 2 3 t dominiq preimagen 7 (no cobrnjectiva) defectiva 1 3 カト recorrido imagen →5 →6 7 3 gectiva) 5 7 1 repaso:28 08 2 3 biyectiva ef 5 7 10 toda función biyectiva tiene reversa". Funciones inyectivas, sobreyectivas y biyectivas: contenidos teóricos, ejercicios resueltos, imágenes, animaciones y formularios de física y matemáticas.

Solution Funci N Inyectiva Sobreyectiva Y Biyectiva Infografia Studypool Una función es inyectiva cuando cada elemento del recorrido es imagen de sólo un elemento del dominio, es decir, ningún elemento del recorrido es imagen de dos preimágenes diferentes. En este artículo explicamos la clasificación de funciones según la relación entre sus elementos en inyectivas, sobreyectivas y biyectivas. analizamos las definiciones, ejemplos, cómo se comportan las gráficas y cómo reconocer a que grupo pertenece una función. Índice función inyectiva función sobreyectiva función biyectiva bibliografía. Las funciones inyectivas, sobreyectivas y biyectivas son las herramientas básicas para comparar el número de elementos de dos conjuntos. observando el digrafo de una función biyectiva f : a !. Una función es inyectiva si a valores distintos que toma la variable independiente le corresponden valores distintos de la variable dependiente. observa los diagramas mostrados a continuación, los cuales representan funciones.

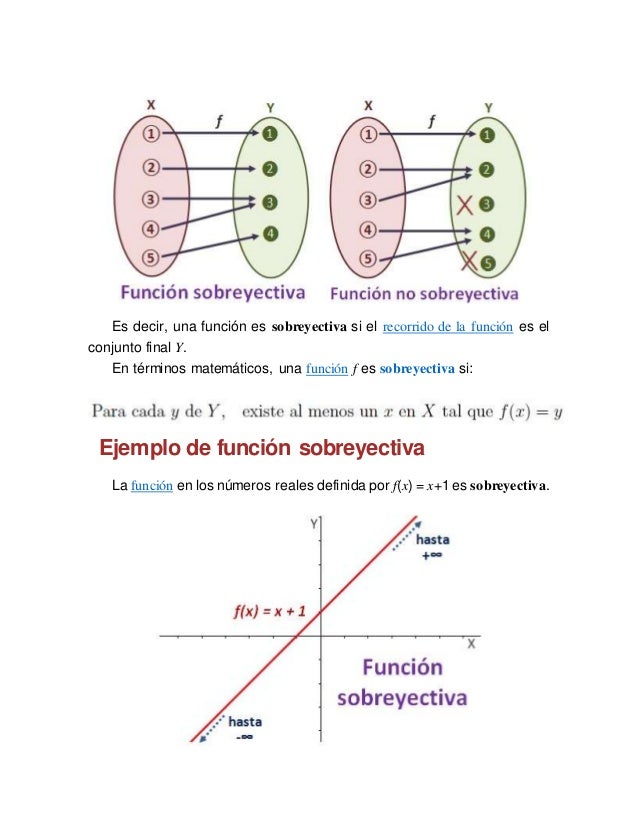
Función Inyectiva Biyectiva Y Sobreyectiva Las funciones inyectivas, sobreyectivas y biyectivas son las herramientas básicas para comparar el número de elementos de dos conjuntos. observando el digrafo de una función biyectiva f : a !. Una función es inyectiva si a valores distintos que toma la variable independiente le corresponden valores distintos de la variable dependiente. observa los diagramas mostrados a continuación, los cuales representan funciones. Gráfica 6: es una función inyectiva porque cada elemento en a se relaciona con un elemento único en b. es sobreyectiva porque cada elemento en b tiene relación con un elemento en a. es biyectiva porque es inyectiva y sobreyectiva. En términos matemáticos, una función f se considera inyectiva si y solo si para cada par de elementos a y b en el dominio, si f (a) = f (b), entonces a = b. existen varias formas de demostrar que una función es inyectiva. una forma común es utilizar el método de la demostración directa, donde asumimos que f (a) = f (b) y demostramos que. Este documento explora en detalle los conceptos de funciones inyectivas (uno a uno), sobreyectivas (suprayectivas u "onto") y biyectivas, proporcionando definiciones formales, ejemplos concretos y representaciones gráficas. A continuación, presentaremos algunos ejemplos prácticos para cada una de estas funciones. empecemos con un ejercicio de función inyectiva. tenemos el conjunto inicial a = {1, 2, 3} y el conjunto final b = {4, 5, 6}. debemos construir una función que cumpla con la condición de inyectividad.

2 1 Ac Tipos De Funciones Inyectiva Sobreyectiva Y Biyectiva Pdf Gráfica 6: es una función inyectiva porque cada elemento en a se relaciona con un elemento único en b. es sobreyectiva porque cada elemento en b tiene relación con un elemento en a. es biyectiva porque es inyectiva y sobreyectiva. En términos matemáticos, una función f se considera inyectiva si y solo si para cada par de elementos a y b en el dominio, si f (a) = f (b), entonces a = b. existen varias formas de demostrar que una función es inyectiva. una forma común es utilizar el método de la demostración directa, donde asumimos que f (a) = f (b) y demostramos que. Este documento explora en detalle los conceptos de funciones inyectivas (uno a uno), sobreyectivas (suprayectivas u "onto") y biyectivas, proporcionando definiciones formales, ejemplos concretos y representaciones gráficas. A continuación, presentaremos algunos ejemplos prácticos para cada una de estas funciones. empecemos con un ejercicio de función inyectiva. tenemos el conjunto inicial a = {1, 2, 3} y el conjunto final b = {4, 5, 6}. debemos construir una función que cumpla con la condición de inyectividad.