Solved Solve The Following Initial Value Problem Chegg Part a) solve the following initial value problem by finding f (x) which satisfies both of the equations: f′ (x)=3x2 8x 4 f (0)=4 part b) calculate f (3) using the function f (x) you found in part a. enter the decimal form of f (3) in the box below, using 3 decimal places. Solve the following initial value problem and find the interval on which the solution is defined (part a). please subscribe and give the video a thumps up!.

Solved Solve The Following Initial Value Problem Chegg 4 problem 1 solve each of the following initial value problems and plot the solutions for several v. lues of y0. then describe in a few words how the solutions resemble, and differ from, 5 = (y 5) divide both s. y0 = 1 y 5 the left side can be written as d=dt(ln jy 5j) by the. Solution the given initial value problem is: x * (dy dx) = sqrt(x^2 4) with the initial condition y(2) = 0. to solve this, we can use the method of separation of variables. this involves rearranging the equation so that all terms involving y are on one side and all terms involving x are on the other. then, we can integrate both sides. First we need to solve the differential equation. if dydx=sinx, d y d x = sin ⁡ x, then. solve the initial value problem dy dx =3x−2, y(1) =2 d y d x = 3 x 2, y (1) = 2. watch the following video to see the worked solution to example: solving an initial value problem and the above try it. For the initial value problem in (8), ti = 2 ih, i.e. t0 = 2:0; t1 = 2:5; t2 = 3:0, and we need to take only two steps, calculating w1 at time t1, and w2 at time t2. we have: the exact solution gives the following values: y(t1 = 2:5) = 1:8333 and y(t2 = 3) = 2:5.

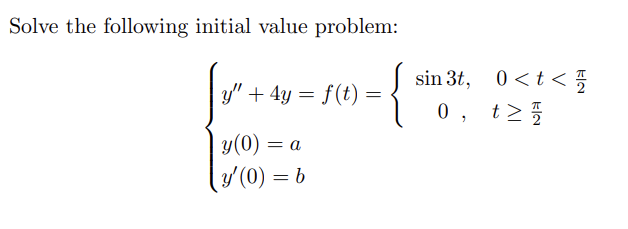
Solved Solve The Following Initial Value Problem Chegg First we need to solve the differential equation. if dydx=sinx, d y d x = sin ⁡ x, then. solve the initial value problem dy dx =3x−2, y(1) =2 d y d x = 3 x 2, y (1) = 2. watch the following video to see the worked solution to example: solving an initial value problem and the above try it. For the initial value problem in (8), ti = 2 ih, i.e. t0 = 2:0; t1 = 2:5; t2 = 3:0, and we need to take only two steps, calculating w1 at time t1, and w2 at time t2. we have: the exact solution gives the following values: y(t1 = 2:5) = 1:8333 and y(t2 = 3) = 2:5. Solution: first, we know f (t; y) = 1 t sin(ty) is continuous on [0; 2] r. second, we can see. so f (t; y) is lipschitz with respect to y (with constant 4). from theorem above, we know the ivp has a unique solution y(t) on [0; 2]. f by (t) and initial value y(a) by change to original solution y(t). let d = [a; b] r. 3. solve the following differential equations or initial value problems. in part (a), leave your answer in implicit form. for parts (b) and (c), write your answer in explicit form. 2 7 (a) y = x (b) y' = (cosa y) int (c) (t2 t) y y2 = ty?, y (1) = 1 y4 – 4y3; y (1) = 2. Applying this formula twice to a c2 function f(t) gives the expression. now, consider the following initial value problem. if we knew how to take the inverse transform of the right hand side we would then have the solution to (2). the table at the end of this section summarizes useful formulas for this purpose. let's take an example. example 1. 0 from problem 2, part (d), form an initial value problem (ivp). a solution to an ivp is a function y(x) that satisfies the given differential equation and has the given initial value.

Solved Solve The Initial Value Problem Find The Soluti Solution: first, we know f (t; y) = 1 t sin(ty) is continuous on [0; 2] r. second, we can see. so f (t; y) is lipschitz with respect to y (with constant 4). from theorem above, we know the ivp has a unique solution y(t) on [0; 2]. f by (t) and initial value y(a) by change to original solution y(t). let d = [a; b] r. 3. solve the following differential equations or initial value problems. in part (a), leave your answer in implicit form. for parts (b) and (c), write your answer in explicit form. 2 7 (a) y = x (b) y' = (cosa y) int (c) (t2 t) y y2 = ty?, y (1) = 1 y4 – 4y3; y (1) = 2. Applying this formula twice to a c2 function f(t) gives the expression. now, consider the following initial value problem. if we knew how to take the inverse transform of the right hand side we would then have the solution to (2). the table at the end of this section summarizes useful formulas for this purpose. let's take an example. example 1. 0 from problem 2, part (d), form an initial value problem (ivp). a solution to an ivp is a function y(x) that satisfies the given differential equation and has the given initial value.

Solved 5 Solve The Following Initial Value Problem Chegg Applying this formula twice to a c2 function f(t) gives the expression. now, consider the following initial value problem. if we knew how to take the inverse transform of the right hand side we would then have the solution to (2). the table at the end of this section summarizes useful formulas for this purpose. let's take an example. example 1. 0 from problem 2, part (d), form an initial value problem (ivp). a solution to an ivp is a function y(x) that satisfies the given differential equation and has the given initial value.