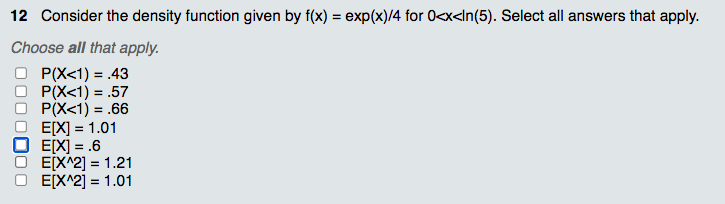
Solved 12 Consider The Density Function Given By F X Chegg

Solved 12 Consider The Density Function Given By F X Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: 12 consider the density function given by f (x) = exp (x) 4 for 0 show transcribed image text. Let x be the continuous random variable with probability density function f (x). for a function to be valid probability function should satisfy below conditions. f (x) should be piecewise continuous. so, the pdf should be the non negative and piecewise continuous function whose total value evaluates to 1. check: normal distribution formula.

Solved Consider The Probability Density Function For F X Chegg The given density function belongs to the exponential family by being expressible in the required form. the variance function is equal to the dispersion parameter, ϕ. the deviance function captures the goodness of fit for the sample data and is evaluated using the provided formula. The function fx(x) f x (x) gives us the probability density at point x x. it is the limit of the probability of the interval (x, x Δ] (x, x Δ] divided by the length of the interval as the length of the interval goes to 0 0. One method is to integrate wrt x x to find the cdf and then differentiate it back wrt y y. another is to use the "change of variable transformation", which involves one differentiation. Find the probability p ( y > x ). p ( y > x ) = p ( 0, 1 ) p ( 1, 2 ) = 0.05 0.05 = 0.10. find p x ), the marginal p.m.f. of x. ↑ the marginal p.m.f. of y. ependent? if not, find cov and y are not independent.

Solved 2 Consider The Density Function F X θxe 2xx2 Chegg One method is to integrate wrt x x to find the cdf and then differentiate it back wrt y y. another is to use the "change of variable transformation", which involves one differentiation. Find the probability p ( y > x ). p ( y > x ) = p ( 0, 1 ) p ( 1, 2 ) = 0.05 0.05 = 0.10. find p x ), the marginal p.m.f. of x. ↑ the marginal p.m.f. of y. ependent? if not, find cov and y are not independent. Answers: 1. for 0 ≤ x ≤ 1 let f(x) = kx(1 − x), where k is a constant. find the value of k such that f is a density function. 2. find the mean and variance of the distribution in the preceding exercise. a. ∫1𝑘𝑘𝑘𝑘(1 −𝑘𝑘)𝑑𝑑𝑘𝑘 0 = 𝑘𝑘 𝑥𝑥 2. T y is uniformly distributed on {0, 1, 2}. let w have the density function f given by f(w. = 2 w3 for w > 1 and f(w) = 0 f. r w ≤ 1. set y = α βw , wh. y ; the quantiles . y ; the mean of y ; the variance of y . let y be a random variable having m. an μ and suppose that e[(y −μ)4] ≤ 2. use this information to determine . Consider the density function given by f (x)et 1tetxtetxxf (x)=1,0. determine the moment generating function of f (x).1tet 1tetxtetxx. your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. To find the constant k in the probability density function f (x) = k √x, we integrate from 0 to 1 and set the result equal to 1. after solving the integral, we determine that k equals 3 2. thus, the correct option is (b) k = 3 2.

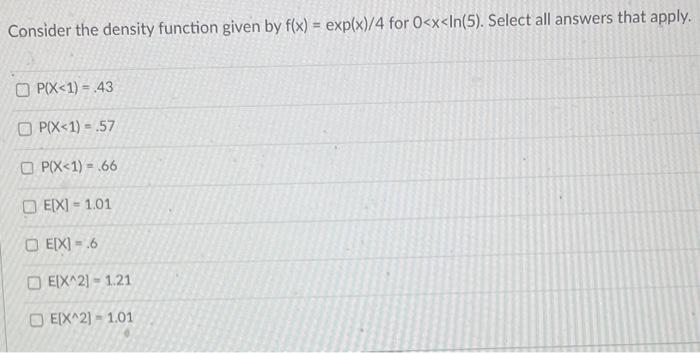
Solved Consider The Density Function Given By F X Exp X 4 Chegg Answers: 1. for 0 ≤ x ≤ 1 let f(x) = kx(1 − x), where k is a constant. find the value of k such that f is a density function. 2. find the mean and variance of the distribution in the preceding exercise. a. ∫1𝑘𝑘𝑘𝑘(1 −𝑘𝑘)𝑑𝑑𝑘𝑘 0 = 𝑘𝑘 𝑥𝑥 2. T y is uniformly distributed on {0, 1, 2}. let w have the density function f given by f(w. = 2 w3 for w > 1 and f(w) = 0 f. r w ≤ 1. set y = α βw , wh. y ; the quantiles . y ; the mean of y ; the variance of y . let y be a random variable having m. an μ and suppose that e[(y −μ)4] ≤ 2. use this information to determine . Consider the density function given by f (x)et 1tetxtetxxf (x)=1,0. determine the moment generating function of f (x).1tet 1tetxtetxx. your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. To find the constant k in the probability density function f (x) = k √x, we integrate from 0 to 1 and set the result equal to 1. after solving the integral, we determine that k equals 3 2. thus, the correct option is (b) k = 3 2.

Discover the Latest Technological Advancements and Trends: Join us on a thrilling journey through the fascinating world of technology. From breakthrough innovations to emerging trends, our Solved 12 Consider The Density Function Given By F X Chegg articles provide valuable insights and keep you informed about the ever-evolving tech landscape.

Sample Question-10: Find the value of k, given a PDF| Chegg Q&A Expert| Probability Density Function

Sample Question-10: Find the value of k, given a PDF| Chegg Q&A Expert| Probability Density Function

Sample Question-10: Find the value of k, given a PDF| Chegg Q&A Expert| Probability Density Function Find the Distribution Function Given the Density Function Solved Problems: Probability Density function What Are Continuous Random Variables? | Introduction to Statistics Find the Mean, Variance, and Standard Deviation Given the Probability Density Function Example of Probability Density Function Numerical Examples on Probability Density Function What is a Probability Density Function (pdf)? ("by far the best and easy to understand explanation") 1 Statistical physics approach to asymptotic enumeration & large deviations in random graphs-Perkins How to Find the Cumulative Distribution Function and Compute the Probabilities given the Density Find the Density Function and Compute the Probabilities Given the Distrubution Function Probability Density Functions: Finding the Mean | Year 12 Maths Methods Find the Mean and Variance of a Random Variable Given the Probability Density Function ECE 302 Lecture 4.1 Probability density functions Lecture 4.5: Probability density function Probability Machine - Galton Board Plinko in Slow Motion with Bell Curve Distribution #statistics Find the Probability Density Function for Continuous Distribution of Random Variable Verifying whether a given function is a probability density function Get the density of Y = X^2 given the pdf of X: a basic example Quantum Wavefunction in 60 Seconds #shorts

Conclusion

After a comprehensive review, it is unmistakable that article gives informative awareness in connection with Solved 12 Consider The Density Function Given By F X Chegg. From start to finish, the commentator reveals remarkable understanding pertaining to the theme. Crucially, the portion covering notable features stands out as a highlight. The content thoroughly explores how these aspects relate to form a complete picture of Solved 12 Consider The Density Function Given By F X Chegg.

Also, the content excels in disentangling complex concepts in an accessible manner. This comprehensibility makes the topic beneficial regardless of prior expertise. The expert further enhances the analysis by introducing applicable examples and concrete applications that frame the theoretical constructs.

Another element that distinguishes this content is the in-depth research of multiple angles related to Solved 12 Consider The Density Function Given By F X Chegg. By investigating these various perspectives, the piece presents a fair perspective of the topic. The comprehensiveness with which the writer handles the issue is highly praiseworthy and provides a model for related articles in this field.

To conclude, this piece not only instructs the audience about Solved 12 Consider The Density Function Given By F X Chegg, but also stimulates additional research into this interesting subject. If you happen to be uninitiated or a specialist, you will find something of value in this detailed write-up. Thanks for reading this comprehensive content. Should you require additional details, feel free to get in touch with the feedback area. I look forward to your feedback. For more information, you will find several relevant publications that you may find helpful and supportive of this topic. Hope you find them interesting!