Solved Curve Sketching Using First And Second Derivative Chegg

Solved Curve Sketching Using First And Second Derivative Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: curve sketching using first and second derivative score: 2 82 8 answered the function f (x)=−4x3−31.32x2 179.9616x−0.26 is increasing on the open interval ( ). it is decreasing on the open interval (−∞,,) and the open interval (,∞). Analyze and sketch a graph using the curve sketching process and using the first and second derivative tests to find extrema and concavity.

Solved Curve Sketching Using First And Second Derivative Chegg Find the local minima and maxima of a function (determine whether a function has a local min or max at a given critical number using the first derivative test and second derivative test). Unit 5 curve sketching. 5.3 determining intervals on which a function is increasing or decreasing. Inflection points occur when the second derivative equals zero and changes sign. concavity of the graph is upward when the second derivative is positive and downward when the second derivative is negative. al xima, minima, inflecti ( ) = 2 − 5. find the first derivative:. The document contains step by step solutions for six practice problems that require taking derivatives of functions and setting them equal to zero to find critical points before determining the overall shape of each graph.

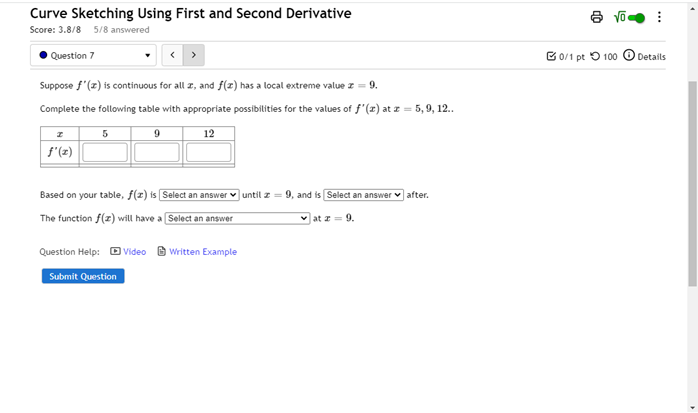
Solved Curve Sketching Using First And Second Derivative Chegg Inflection points occur when the second derivative equals zero and changes sign. concavity of the graph is upward when the second derivative is positive and downward when the second derivative is negative. al xima, minima, inflecti ( ) = 2 − 5. find the first derivative:. The document contains step by step solutions for six practice problems that require taking derivatives of functions and setting them equal to zero to find critical points before determining the overall shape of each graph. We have shown how to use the first and second derivatives of a function to describe the shape of a graph. now we put everything together with other features to graph a function . Sketch the curve represented by the given function by finding critical values (local minimum, local maximum points and general extrema) and inflection points by analyzing first and second derivative functions. Question: curve sketching using first and second derivatives for the function given, show all work to find: relative extrema intervals of increase and decrease point (s) of concavity inflection intervals of concavity y intercept then sketch the graph of the original f (x) function, including labels for all above points. Goal: use rst and second derivatives to make a rough sketch of the graph of a function f (x). critical points: points c in the domain of f (x) where f 0(c) does not exist or f 0(c) = 0. 0(x) > 0 ) f (x) increasing. 0(x) < 0 ) f (x) decreasing.

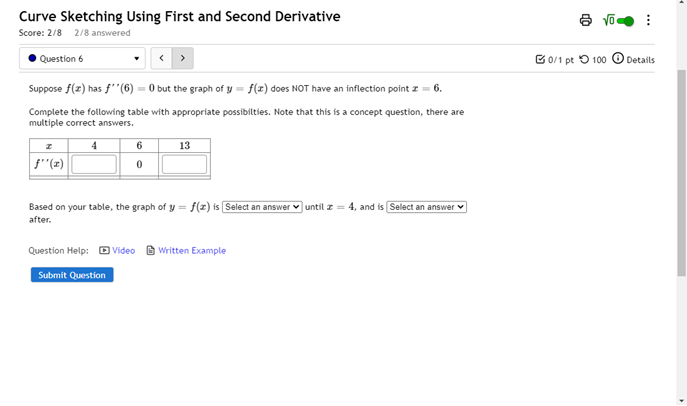
Solved Curve Sketching Using First And Second Derivative Chegg We have shown how to use the first and second derivatives of a function to describe the shape of a graph. now we put everything together with other features to graph a function . Sketch the curve represented by the given function by finding critical values (local minimum, local maximum points and general extrema) and inflection points by analyzing first and second derivative functions. Question: curve sketching using first and second derivatives for the function given, show all work to find: relative extrema intervals of increase and decrease point (s) of concavity inflection intervals of concavity y intercept then sketch the graph of the original f (x) function, including labels for all above points. Goal: use rst and second derivatives to make a rough sketch of the graph of a function f (x). critical points: points c in the domain of f (x) where f 0(c) does not exist or f 0(c) = 0. 0(x) > 0 ) f (x) increasing. 0(x) < 0 ) f (x) decreasing.

Immerse Yourself in Art, Culture, and Creativity: Celebrate the beauty of artistic expression with our Solved Curve Sketching Using First And Second Derivative Chegg resources. From art forms to cultural insights, we'll ignite your imagination and deepen your appreciation for the diverse tapestry of human creativity.

Given fx sketch the first and second derivative graph

Given fx sketch the first and second derivative graph

Given fx sketch the first and second derivative graph Curve Sketching - First & Second Derivatives - Graphing Rational Functions & Asymptotes - Calculus Ap Calculus AB Curve Sketching First and Second Derivative Test Ti-Nspire curve sketching using first and second derivative Sketching a Graph Using First and Second Derivative Tests Calculus Curve Sketching From Given First and Second Derivatives Curve Sketching using Calculus First and Second Derivative Math 121: Curve sketching using first and second derivative tests curve sketching using first and second derivative Curve Sketching Using The First And Second Derivatives Curve Sketching Using First and Second Derivatives Sketch Graph from Given Information of first and second derivative Extremely Important IBSL Calculus Calculus - Curve Sketching using the First and Second Derivative Curve Sketching Using the First and Second Derivative – Geometrical Application of Calculus Needham Calculus: Curve Sketching Using Derivatives Curve Sketching Using the first and second derivative Curve sketching using first and second derivatives Curve sketching using first and second derivatives 1151 FF: Curve Sketching from 1st Derivative Curve Sketching Using Derivatives

Conclusion

After a comprehensive review, there is no doubt that this specific write-up presents helpful understanding pertaining to Solved Curve Sketching Using First And Second Derivative Chegg. In every section, the blogger demonstrates considerable expertise about the area of interest. Particularly, the discussion of fundamental principles stands out as exceptionally insightful. The presentation methodically addresses how these components connect to build a solid foundation of Solved Curve Sketching Using First And Second Derivative Chegg.

Furthermore, the piece is impressive in disentangling complex concepts in an straightforward manner. This clarity makes the information useful across different knowledge levels. The content creator further elevates the presentation by weaving in related instances and tangible use cases that frame the theoretical constructs.

One more trait that makes this piece exceptional is the comprehensive analysis of multiple angles related to Solved Curve Sketching Using First And Second Derivative Chegg. By investigating these different viewpoints, the post provides a balanced understanding of the topic. The completeness with which the writer approaches the matter is genuinely impressive and sets a high standard for similar works in this subject.

In summary, this content not only teaches the viewer about Solved Curve Sketching Using First And Second Derivative Chegg, but also motivates continued study into this fascinating topic. If you are new to the topic or a veteran, you will find useful content in this detailed piece. Gratitude for reading this detailed piece. If you would like to know more, you are welcome to drop a message with our messaging system. I anticipate your feedback. To deepen your understanding, you can see some associated pieces of content that are interesting and supportive of this topic. Enjoy your reading!