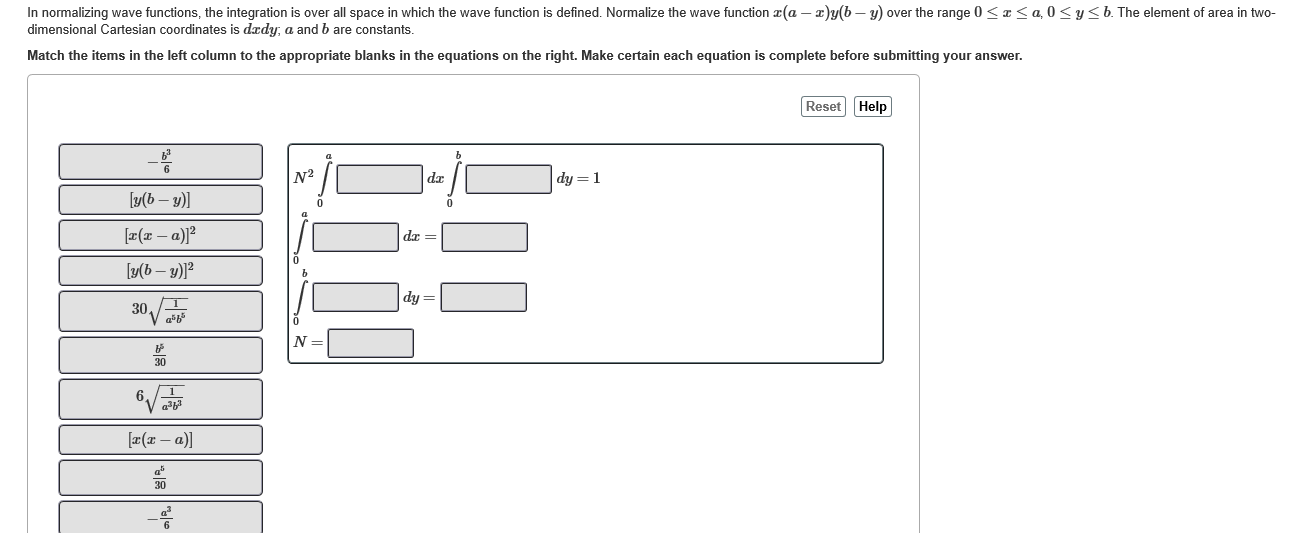
Solved In Normalizing Wave Functions The Integration Is Over

Solved In Normalizing Wave Functions The Integration Is Chegg In normalizing wave functions, the integration is over all space in which the wave function is defined. normalize the wave function x (a−x)y (b−y) x (a−x)y (b−y) over the range 0≤x≤a 0≤x≤a , 0≤y≤b 0≤y≤b . the element of area in two dimensional cartesian coordinates is dx dx dy dy ; a a and b b are constants. When normalizing a wave function, integration is used to calculate the total probability by summing up the probabilities over all space. this involves integrating the square of the wave function's modulus.

In Normalizing Wave Functions The Integration Is Chegg Hence, we conclude that all wavefunctions that are square integrable [i.e., are such that the integral in equation ([e3.4]) converges] have the property that if the normalization condition ([e3.4]) is satisfied at one instant in time then it is satisfied at all subsequent times. Normalizing the wave function means probability of finding an electron in limited area (i.e. somewhere in space) is one. so, the normalization is possible when there are some boundary conditions placed on the particle. Find step by step chemistry solutions and your answer to the following textbook question: in normalizing wave functions, the integration is over all space in which the wave function is defined. a. normalize the wave function $x (a x) y (b y)$ over the range $0 \leq x \leq a, 0 \leq y \leq b$. To normalize the wave function x(a − x)y(b − y) x ( a − x) y ( b − y), we need to find the constant n n such that the integral of the square of the wave function over the given range is equal to 1.

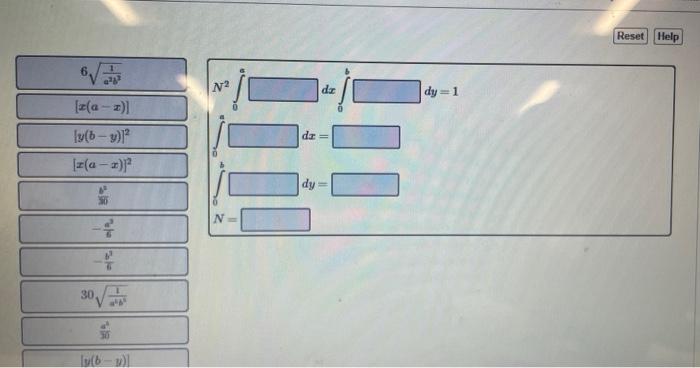
Solved In Normalizing Wave Functions The Integration Is Chegg Find step by step chemistry solutions and your answer to the following textbook question: in normalizing wave functions, the integration is over all space in which the wave function is defined. a. normalize the wave function $x (a x) y (b y)$ over the range $0 \leq x \leq a, 0 \leq y \leq b$. To normalize the wave function x(a − x)y(b − y) x ( a − x) y ( b − y), we need to find the constant n n such that the integral of the square of the wave function over the given range is equal to 1. Determine the value that a (assumed real) must have if the wavefunction is to be correctly normalised, i.e. the volume integral of |Ψ|2 over all space is equal to unity. Question: in normalizing wave functions, the integration is over all space in which the wave function is defined. a. normalize the wave function x (a − x) y (b − y) over the range 0 ≤ x ≤ a, 0 ≤ y ≤ b. the element of area in two dimensional cartesian coordinates is dx dy; a and b are constants. b. These look like infinite square well wave functions so the limits should be [0, 1] [0, 1] or perhaps one of a few other choices of bounded interval. (it could also be a free particle, but this combination cannot be normalized it integrates to infinity.). In normalizing wave functions, the integration is over all space in which the wave function is defined. the following examples allow you to practice your skills in two and three dimensional integration. normalize the wave function sin (n pi x a) sin (m pi y b) over the range 0. your solution’s ready to go!.

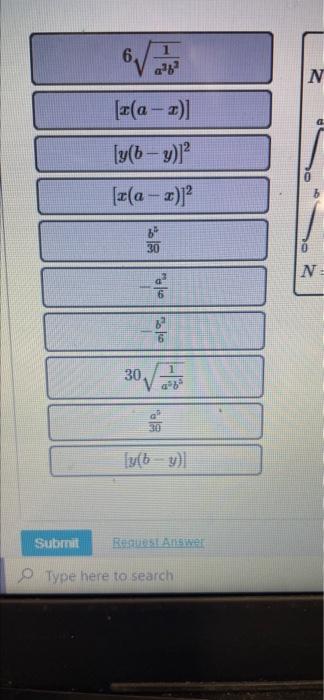
Solved In Normalizing Wave Functions The Integration Is Chegg Determine the value that a (assumed real) must have if the wavefunction is to be correctly normalised, i.e. the volume integral of |Ψ|2 over all space is equal to unity. Question: in normalizing wave functions, the integration is over all space in which the wave function is defined. a. normalize the wave function x (a − x) y (b − y) over the range 0 ≤ x ≤ a, 0 ≤ y ≤ b. the element of area in two dimensional cartesian coordinates is dx dy; a and b are constants. b. These look like infinite square well wave functions so the limits should be [0, 1] [0, 1] or perhaps one of a few other choices of bounded interval. (it could also be a free particle, but this combination cannot be normalized it integrates to infinity.). In normalizing wave functions, the integration is over all space in which the wave function is defined. the following examples allow you to practice your skills in two and three dimensional integration. normalize the wave function sin (n pi x a) sin (m pi y b) over the range 0. your solution’s ready to go!.

Solved In Normalizing Wave Functions The Integration Is Chegg These look like infinite square well wave functions so the limits should be [0, 1] [0, 1] or perhaps one of a few other choices of bounded interval. (it could also be a free particle, but this combination cannot be normalized it integrates to infinity.). In normalizing wave functions, the integration is over all space in which the wave function is defined. the following examples allow you to practice your skills in two and three dimensional integration. normalize the wave function sin (n pi x a) sin (m pi y b) over the range 0. your solution’s ready to go!.

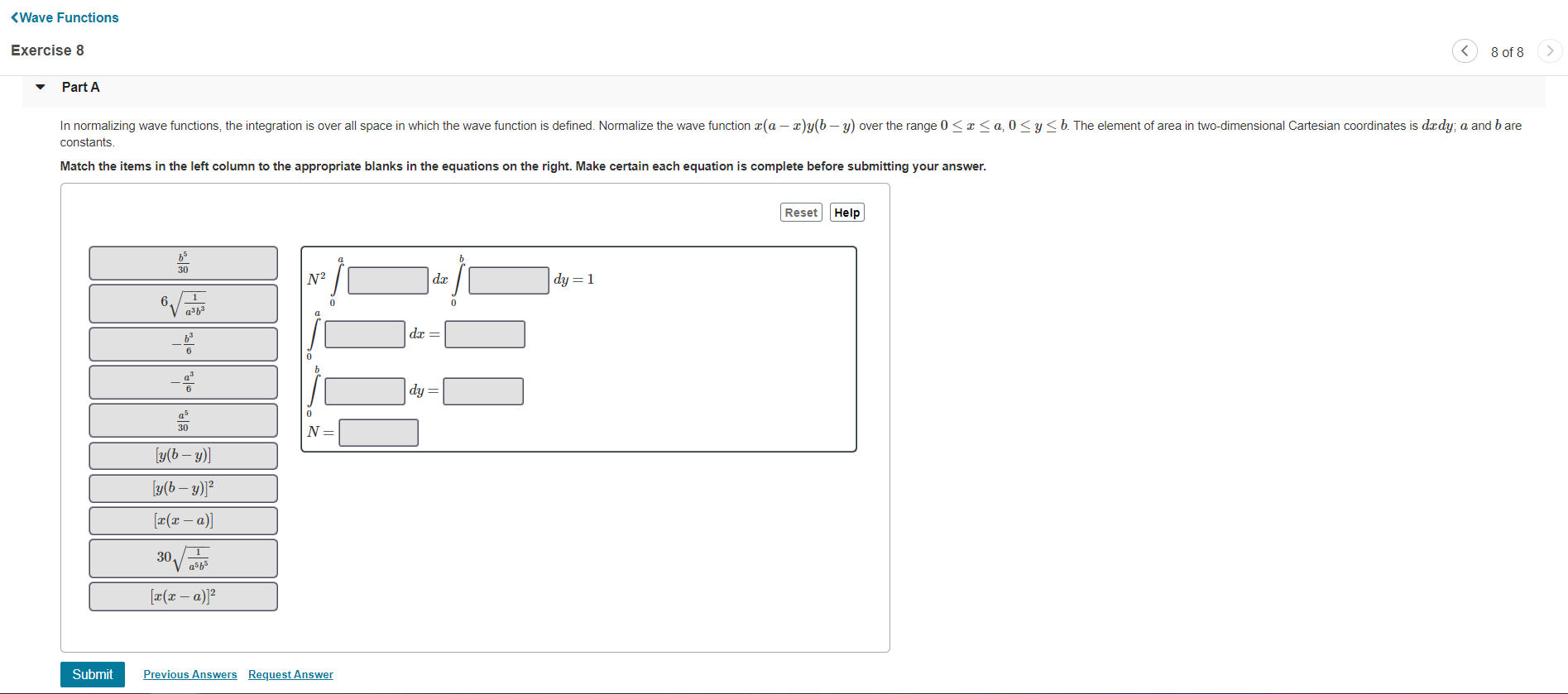
Solved Part A In Normalizing Wave Functions The Chegg

Delight Your Taste Buds with Exquisite Culinary Adventures: Explore the culinary world through our Solved In Normalizing Wave Functions The Integration Is Over section. From delectable recipes to culinary secrets, we'll inspire your inner chef and take your cooking skills to new heights.

How to Normalize a Wave function in Quantum Mechanics

How to Normalize a Wave function in Quantum Mechanics

How to Normalize a Wave function in Quantum Mechanics Wavefunction Properties, Normalization, and Expectation Values Wavefunction Normalization Doesn’t Change Over Time – Here's the Proof! Normalizing Wavefunctions in the Position Representation Why We Need the Normalization Condition in Quantum Mechanics How to Normalize a Wave Function Wave Function Constraints and Normalization Normalization of the Wavefunction | Physical Chemistry II | 2.6 Normalization Griffiths Problem 1.7: Normalizing a Piecewise Wavefunction Wavefunction Normalization Example | Physical Chemistry II | 2.7 The LAST STEP in QUANTUM MECHANICAL Wave Function Calculations | Normalization of the Wave Function Normalization of wave function, Solved problem on normalization, Quantum Mechanics How to normalize a wavefunction - Real Chemistry Rigid Rotor - Normalization Normalising a Wave Function (PhysCasts) Normalizable wavefunctions and the question of time evolution How to Normalize Wave Function? | Calculate "Normalization Constant" | Quantum Mechanics PROOF that Normalization is Preserved with Time Normalizing a Wavefunction

Conclusion

Having examined the subject matter thoroughly, it can be concluded that write-up gives beneficial information touching on Solved In Normalizing Wave Functions The Integration Is Over. From beginning to end, the scribe depicts noteworthy proficiency about the area of interest. Specifically, the part about notable features stands out as extremely valuable. The writer carefully articulates how these aspects relate to develop a robust perspective of Solved In Normalizing Wave Functions The Integration Is Over.

On top of that, the post is commendable in breaking down complex concepts in an clear manner. This clarity makes the topic beneficial regardless of prior expertise. The expert further strengthens the analysis by embedding suitable instances and real-world applications that place in context the abstract ideas.

Another element that sets this article apart is the detailed examination of diverse opinions related to Solved In Normalizing Wave Functions The Integration Is Over. By exploring these various perspectives, the post delivers a well-rounded perspective of the theme. The comprehensiveness with which the author tackles the matter is truly commendable and sets a high standard for similar works in this domain.

To summarize, this write-up not only enlightens the reader about Solved In Normalizing Wave Functions The Integration Is Over, but also motivates continued study into this fascinating area. Whether you are a beginner or an authority, you will uncover useful content in this exhaustive article. Thank you for reading this detailed content. Should you require additional details, you are welcome to contact me via our contact form. I am eager to your feedback. For further exploration, here is some relevant write-ups that are useful and supplementary to this material. Happy reading!