
Solved Finding The Standard Matrix And The Image In Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: problem 10. find the standard matrix for the following linear transformations from r2 to r2. then determine whether the matrix is invertible or not. If you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is sufficient to obtain the matrix of your linear transformation.

Solved Problem Find The Matrix Which Represents In Standard Chegg Thus we have two distinct eigenvalues 1 = 1 and 2 = 2 and as a result the corresponding eigenvalues are linearly independent and the matrix a is diagonalizable. If you use brute force computation to solve the system of 9 equations in 9 unknowns (later theorems will remove some of the work), you can show that the only matrices b that commute with a are those that can be written as aa2 ba ci3 for some numbers a; b; c. Row reduce the matrix [at : bt] (note the transpose!!!) to [in : m]. then mt is the matrix mt . example. given t = (again, note the transposing!). this row reduces to:. Say the matrix a has a simple eigenvalue 0 and corresponding eigenvector ~v0. show there is no vector ~z linearly independent of ~v0 with the property a~z = 0~z c~v0 for any value of the scalar c.
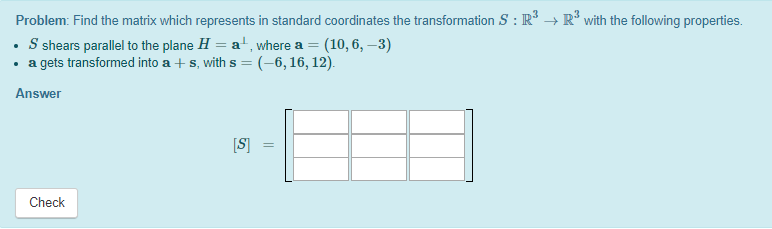
Solved Problem Find The Matrix Which Represents In Standard Chegg Row reduce the matrix [at : bt] (note the transpose!!!) to [in : m]. then mt is the matrix mt . example. given t = (again, note the transposing!). this row reduces to:. Say the matrix a has a simple eigenvalue 0 and corresponding eigenvector ~v0. show there is no vector ~z linearly independent of ~v0 with the property a~z = 0~z c~v0 for any value of the scalar c. Elementary linear algebra version howard anton, chris rorres 10 edition chapter 4, problem 20. Join today and access millions of expert created videos, each one skillfully crafted to teach you how to solve tough problems step by step. Problem 10. 8 marks] given the following linear transformations, 1. find the standard matrix of transformation f:r2 r2 the reflection of a point in the x axis. Theorem 6.3.3 suppose t1 : rn → rm, t2 : rm rp → ar 2 is the standard matrix of t2. then, the st t2ot1 is the product.