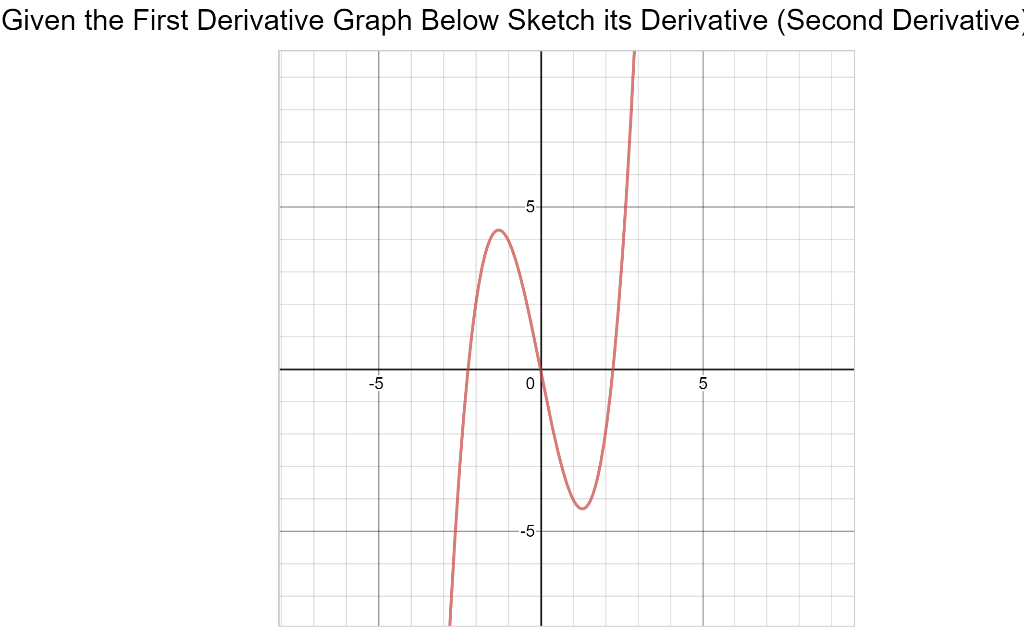
Solved Given The First Derivative Graph Below Sketch Its Chegg The following problems illustrate detailed graphing of functions of one variable using the first and second derivatives. problems range in difficulty from average to challenging. Analyze and sketch a graph using the curve sketching process and using the first and second derivative tests to find extrema and concavity.

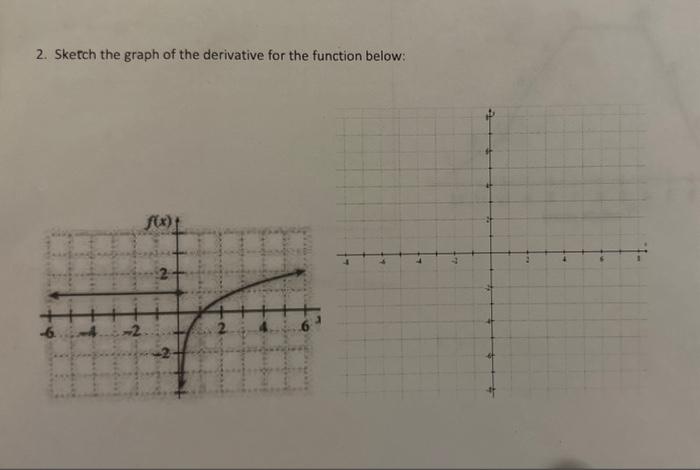
Solved Sketch The Graph Of The Derivative For The Function Chegg For example, f(x) is a cubic polynomial (degree 3), then its derivative function is quadratic (degree 2). the derivative of the quadratic function is linear, so the second derivative function of a cubic polynomial is linear (degree 1). Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. as extraction of the exact equation of given cur … not the question you’re looking for? post any question and get expert help quickly. A tutorial on how to use the first and second derivatives, in calculus, to study the properties of the graphs of functions. to graph functions in calculus we first review several theorem. Explains how to use the graph of a function to sketch the graphs of the first and second derivative of that function.

Answered Use First And Second Derivative Information To Sketch The A tutorial on how to use the first and second derivatives, in calculus, to study the properties of the graphs of functions. to graph functions in calculus we first review several theorem. Explains how to use the graph of a function to sketch the graphs of the first and second derivative of that function. Rts for a function g and its first two derivatives are given. a black dot repr ents a zero, and a white dot represents a vertical asymptote. assume that the graph of g has a vertical asymptote at x. The very first practice problem asked you to incorporate slope information into a sketch. sketching is as much an art as a science, but there are methodical ways to use information about the function and its derivatives. We have shown how to use the first and second derivatives of a function to describe the shape of a graph. now we put everything together with other features to graph a function . we now have enough analytical tools to draw graphs of a wide variety of algebraic and transcendental functions. In figure 4.3 4.3 we show the functions y(t) y (t) (top row), their first derivatives y′(t) y ′ (t) (middle row), and the second derivatives y′′(t) y ′ ′ (t) (bottom row).