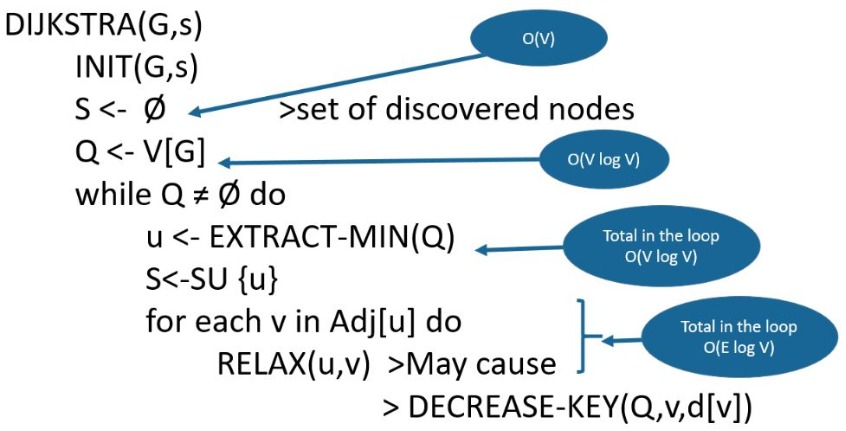
Understanding Time Complexity Calculation For Dijkstr Vrogue Co In this tutorial, we’ll learn the concept of dijkstra’s algorithm to understand how it works. at the end of this tutorial, we’ll calculate the time complexity and compare the running time between different implementations. 2. the algorithm. The time complexity of dijkstra's algorithm is typically o (v2) when using a simple array implementation or o ( (v e) log v) with a priority queue, where v represents the number of vertices and e represents the number of edges in the graph.

Understanding Time Complexity Calculation For Dijkstr Vrogue Co Since with dijkstra's algorithm you have o (n) delete min s and o (m) decrease key s, each costing o (logn), the total run time using binary heaps will be o (log (n) (m n)). This blog provides a deeper dive into the time complexity analysis of dijkstra’s algorithm and aims to provide a better understanding of the nuances of using different data structures. Learn the dijkstra algorithm with a detailed example, time complexity analysis, and implementation code. perfect guide for mastering shortest path algorithms!. In this article, we have explored the time & space complexity of dijkstra's algorithm including 3 different variants like naive implementation, binary heap priority queue and fibonacci heap priority queue.

Understanding Time Complexity Calculation For Dijkstr Vrogue Co Learn the dijkstra algorithm with a detailed example, time complexity analysis, and implementation code. perfect guide for mastering shortest path algorithms!. In this article, we have explored the time & space complexity of dijkstra's algorithm including 3 different variants like naive implementation, binary heap priority queue and fibonacci heap priority queue. In this article, we have analyzed the time complexity of a dijkstra’s algorithm calculator. the analysis shows that the algorithm has a time complexity of o (n log n), making it suitable for large scale networks. Dijkstra's algorithm is a widely used algorithm for finding the shortest path between nodes in a weighted graph. in this article, we will delve into the time complexity of dijkstra's algorithm. Every time you find an optimized route, there’s a high chance dijkstra’s algorithm (or one of its cousins) had a say. before we jump to code, let’s break down some terms: weighted graph: a network of nodes (points) and edges (paths) where each edge has a weight (distance, time, cost). Key takeaways let‘s review the core points: 💡 dijkstra‘s algorithm finds the shortest path from a source node to all other nodes via a greedy breadth first approach 💡 it uses a priority queue to visit closest nodes first to incrementally build solution 💡 time complexity is o (e log v) using common graph and queue representations.