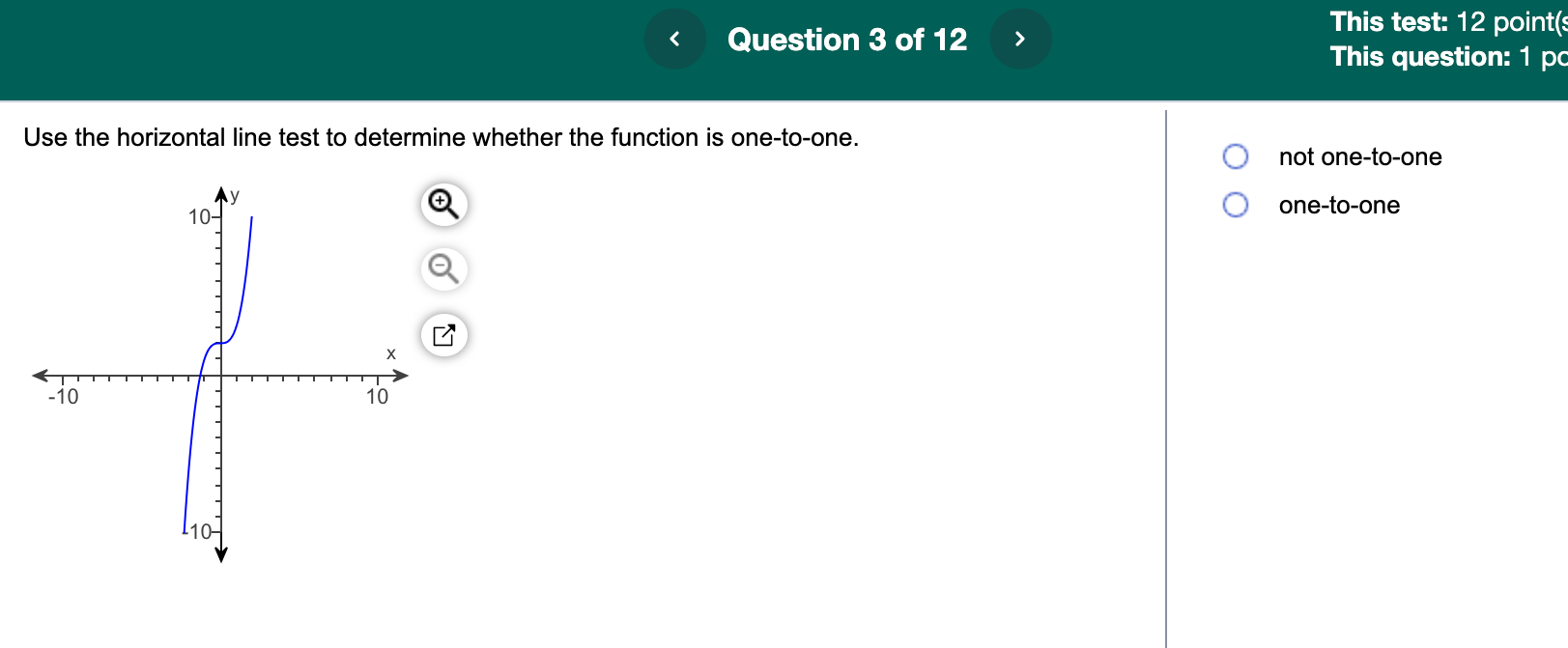
Solved Use The Horizontal Line Test To Determine Whether The Chegg The horizontal line test is a simple visual technique that shows if a function is one to one. learn to use it with lots of examples and practice. In this section we’ll talk about how to determine whether a graph represents a one to one function. if a relation is a function, then it has exactly one y value for each x value.

Answered Use The Horizontal Line Test To Determine Whether The Kunduz This precalculus video tutorial explains how to determine if a graph has an inverse function using the horizontal line test. if it passes the test, the function is a one to one. Step by step tutorial explains how to determine if a function is a one to one function using the horizontal line test. ace your math exam!. Given a graph of a function, use the horizontal line test to determine if the graph represents a one to one function. inspect the graph to see if any horizontal line drawn would intersect the curve more than once. To determine that whether the function f (x) is a one to one function or not, we have two tests. 1) horizontal line testing: if the graph of f (x) passes through a unique value of y every time, then the function is said to be one to one function. for example let f (x) = x 3 1 and g (x) = x 2 1.

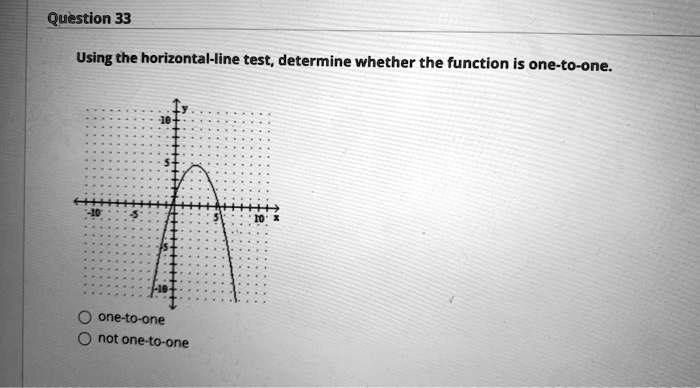
Solved Question 33 Using The Horizontal Line Test Determine Whether Given a graph of a function, use the horizontal line test to determine if the graph represents a one to one function. inspect the graph to see if any horizontal line drawn would intersect the curve more than once. To determine that whether the function f (x) is a one to one function or not, we have two tests. 1) horizontal line testing: if the graph of f (x) passes through a unique value of y every time, then the function is said to be one to one function. for example let f (x) = x 3 1 and g (x) = x 2 1. To determine if a function is one to one, we can use the horizontal line test. the horizontal line test – plain and simple – tells us whether or not the inverse is a function. Using the horizontal line test, indicate whether the following function is one to one: f (x) = x 3 1 f (x) = x3 −1 solution: in order to assess whether or not the given function passes the horizontal line test, we need to solve the equation y = x 3 1 y = x3−1 for x x and determine whether there is no solution, one solution, or multiple. One very important classification is deciding whether a function is one to one. you can do this using graphing techniques called vertical and horizontal line tests. a function is one to one if it has exactly one output value for every input value and exactly one input value for every output value. formally, you write this definition as follows:. The video has two examples and a definition of one to one. i talk about the technique of the horizontal line test and its application of the definition of 1 1. i do talk about notation for.

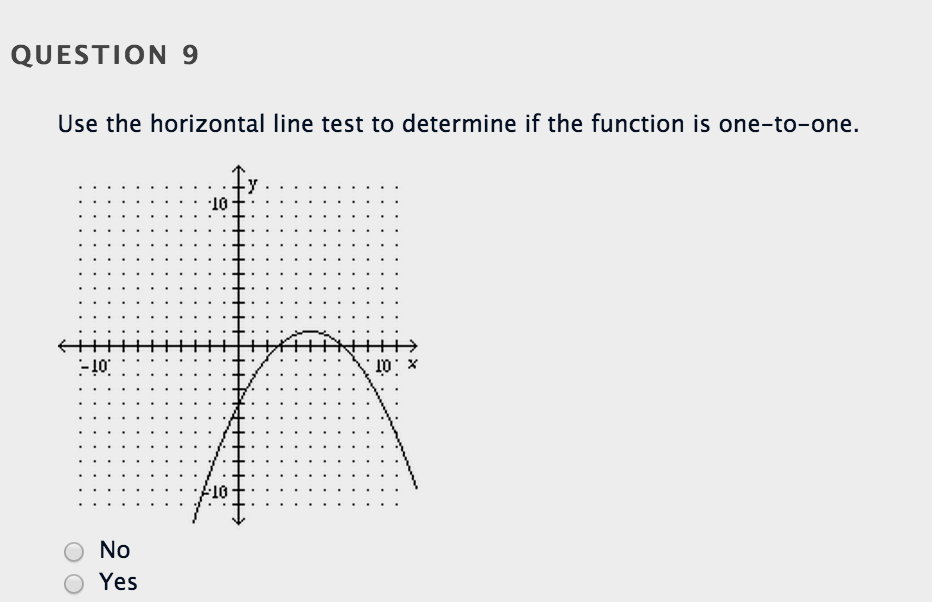
Solved Use The Horizontal Line Test To Determine If The Chegg To determine if a function is one to one, we can use the horizontal line test. the horizontal line test – plain and simple – tells us whether or not the inverse is a function. Using the horizontal line test, indicate whether the following function is one to one: f (x) = x 3 1 f (x) = x3 −1 solution: in order to assess whether or not the given function passes the horizontal line test, we need to solve the equation y = x 3 1 y = x3−1 for x x and determine whether there is no solution, one solution, or multiple. One very important classification is deciding whether a function is one to one. you can do this using graphing techniques called vertical and horizontal line tests. a function is one to one if it has exactly one output value for every input value and exactly one input value for every output value. formally, you write this definition as follows:. The video has two examples and a definition of one to one. i talk about the technique of the horizontal line test and its application of the definition of 1 1. i do talk about notation for.